The vast majority of differential equations that occur in electrodynamics (and quantum theory via the Schr\”odinger equation) are a class of homogeneous second order equations called the Sturm-Liouville equation. The solutions to these equations are generally polynomials ![]() with a set of remarkable properties:
with a set of remarkable properties:
![]() They are orthogonal with respect to a weight function over
They are orthogonal with respect to a weight function over ![]() ;
;
![]()
which means that they can be regarded as a basis of the infinite dimensional space of functions on ![]() ;
;
![]()
(the Fourier-Dini series).
![]() They can be generated from a simple formula
They can be generated from a simple formula
![]()
called a Rodriguez formula.
![]() The Rodriguez formula can be turned into a generating function
The Rodriguez formula can be turned into a generating function
![]()
the right-side of which can be found explicitly using the Cauchy theorem (and by other methods).
Let’s construct functions that have precisely these properties, and in the process obtain the general form of the Sturm-Liouville equation
![]()
![]()
with polynomial solutions ![]() of order
of order ![]() . Nearly every special function that we know and love falls into this category (to name just a few):
. Nearly every special function that we know and love falls into this category (to name just a few):
![Rendered by QuickLaTeX.com \[ \begin{array}{l|l|l|l|l}\mbox{Equation}&A&B&\lambda & \mbox{Name}\\ \hline (1-x^2)\rho''-2x\rho'+n(n+1)\rho=0&(1-x^2)&0&-n(n+1)&\mbox{Legendre}, \, P_n\\ &&&&\\ \rho''-2x\rho'+2n\rho=0& 1 &-2x &-2n&\mbox{Hermite}, \, H_n\\ &&&&\\ x\rho''+(a+1-x)\rho'+n\rho=0& x &(a-x) &-n&\mbox{Laguerre}, \, L_n^a\\ &&&&\\ (1-x^2)\rho''-x\rho'+n^2\rho=0& (1-x^2) &x &n^2&\mbox{Chebyshev}, \, T_n\\ \end{array}\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-7e790b49bb3c92a0aa9a37c9f3921935_l3.png)
Let’s begin by finding the differential equation whose solution is ![]() , for
, for ![]() (you will see that this is needed to make the final solutions polynomials);
(you will see that this is needed to make the final solutions polynomials);
(1) 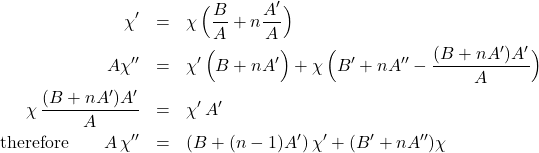
This is a Sturm-Liouville equation if ![]() is constant (
is constant (![]() no higher than first order,
no higher than first order, ![]() no higher than quadratic). Let this be so, now differentiate the entire equation
no higher than quadratic). Let this be so, now differentiate the entire equation ![]() times, calling
times, calling ![]()
(2) 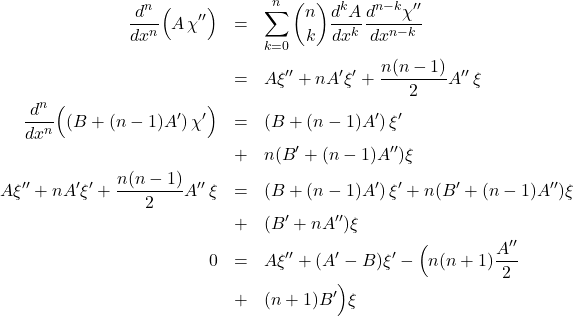
This is another Sturm-Liouville equation if ![]() is constant.
is constant.
Now let ![]() ;
;
(3) 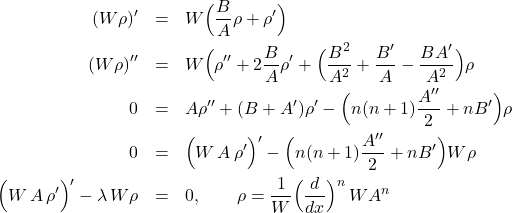
the standard Sturm-Liouville form with its polynomial solution given by a Rodriguez formula, and the explicit eigenvalue ![]() .
.
Suppose that ![]() and
and ![]() , vanishing faster at
, vanishing faster at ![]() (
(![]() ) than any power of
) than any power of ![]() . Notice that if both
. Notice that if both ![]() and
and ![]() are polynomials in
are polynomials in ![]() ,
,
(4) 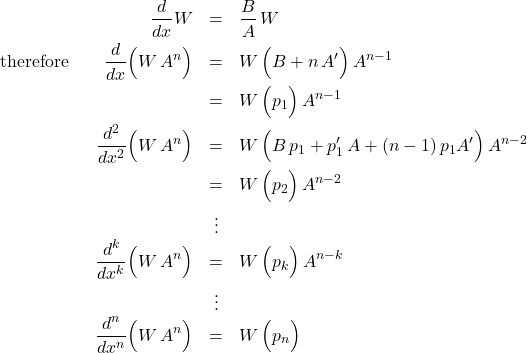
then ![]() are all polynomials in
are all polynomials in ![]() . If
. If ![]() is no higher order than first, and
is no higher order than first, and ![]() no higher order than second, then
no higher order than second, then ![]() is a polynomial of order
is a polynomial of order ![]() . You can see this by simply counting orders of the parts of each
. You can see this by simply counting orders of the parts of each ![]() .
.
We have established that if ![]() is no higher order than first, and
is no higher order than first, and ![]() no higher order than second, then
no higher order than second, then
![]()
is a polynomial of order ![]() . The most important property of these polynomials is that they are orthogonal on the interval
. The most important property of these polynomials is that they are orthogonal on the interval ![]() with weight function
with weight function ![]() : let
: let ![]()
(5) 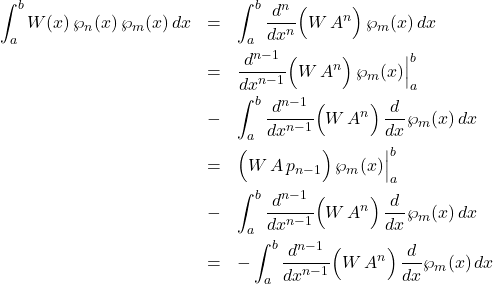
the first term vanishing because ![]() and
and ![]() vanish strongly at the endpoints of the domain. Repeat the process
vanish strongly at the endpoints of the domain. Repeat the process
(6) 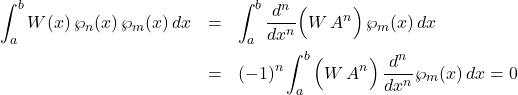
since the ![]() derivative of a polynomial of order less than
derivative of a polynomial of order less than ![]() is zero.
is zero.
Theorem
The Sturm-Liouville equation
![]()
has polynomial solutions of order ![]() orthogonal on
orthogonal on ![]() with respect to weight function
with respect to weight function
![]()
provided ![]() vanishes strongly at
vanishes strongly at ![]() ,
, ![]() is at most quadratic
is at most quadratic ![]() ,
, ![]() is at most linear
is at most linear ![]() , and
, and
![]()
and under these conditions the polynomial solutions are\index{Rodriguez formula}
![]()
What this means to you is that when you solve a problem by variable separation and one of the resulting ordinary DE’s is a Sturm-Liouville type, then you can do “Fourier” expansions (actually they are called Fourier-Dini in this case) to solve for all of the coefficients. We will do this with Legendre and associated Legendre which pertain to spherical coordinate boundary value problems, but in your quantum, em and cm courses you will use many other SL-equations.
Suggested reading and reference: Special Functions by N. N. Lebedev.