Physics 7XX: The virial theorem

Consider the quantity

$Q=\sum_j\mathbf{p}_j\cdot\mathbf{r}_j$

summed over the particles in a system. Assume that each particle ( $j$ ) is subjected to external forces $\mathbf{F}_{j, ext}$ and internal interparticle forces, exerted for example by particle $k$ through potentials

$V(\mathbf{r}_j-\mathbf{r}_k)=a \, |\mathbf{r}_j-\mathbf{r}_k|^\nu$

This is why $Q$ is significant:

$\dot{Q}=2 \, T-\nu V+\sum_j \mathbf{F}_{j,ext}\cdot\mathbf{r}_j$

{\bf Proof}.

(1) $\begin{eqnarray*}\dot{Q}&=&\sum_j\dot{\mathbf{p}}_j\cdot\mathbf{r}_j+\sum_j\mathbf{p}_j\cdot\dot{\mathbf{r}}_j\nonumber\\ &=&\sum_j\mathbf{F}_j\cdot\mathbf{r}_j+\sum_j\mathbf{p}_j\cdot\dot{\mathbf{r}}_j\nonumber\\ &=&\sum_j\mathbf{F}_{j,int}\cdot\mathbf{r}_j+\sum_j\mathbf{F}_{j,ext}\cdot\mathbf{r}_j+\sum_j\mathbf{p}_j\cdot\dot{\mathbf{r}}_j\nonumber\end{eqnarray*}$

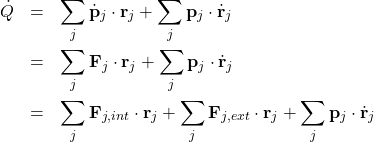
The last term is the kinetic energy

$\sum_j\mathbf{p}_j\cdot\dot{\mathbf{r}}_j=\sum_j{1\over m_j}\mathbf{p}_j\cdot\dot{\mathbf{p}}_j=2 \, T$

The first is the potential energy for the potentials

$V(\mathbf{r}_j-\mathbf{r}_k)=a \, |\mathbf{r}_j-\mathbf{r}_k|^\nu, \qquad\mathbf{F}_j=-\nu a\sum_{k\ne j}(\mathbf{r}_j-\mathbf{r}_k) \, |\mathbf{r}_j-\mathbf{r}_k|^{\nu-2}$

then

(2) $\begin{eqnarray*} \sum_j\mathbf{F}_j\cdot\mathbf{r}_j&=&-\nu a\sum_j\sum_{k\ne j}(\mathbf{r}_j-\mathbf{r}_k)\cdot\mathbf{r}_j \, |\mathbf{r}_j-\mathbf{r}_k|^{\nu-2}\nonumber\\ &=&-\nu a\sum_j\sum_{k< j}(\mathbf{r}_j-\mathbf{r}_k)\cdot(\mathbf{r}_j-\mathbf{r}_k) \, |\mathbf{r}_j-\mathbf{r}_k|^{\nu-2}\nonumber\\ &=&-\nu \sum_j\sum_{k< j} V(\mathbf{r}_j-\mathbf{r}_k)=-\nu \, V\nonumber\end{eqnarray*}$

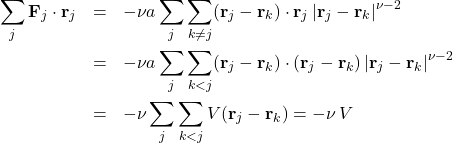
Next we show that

$\dot{Q}=2 \, T-\nu V-3P_{ext,total} \, Vol$

if the system is enclosed in a box and the walls are under external pressure. A particle on a wall will experience $\mathbf{F}_{j,ext}=-P_{ext,1}A_{wall} \mathbf{n}$ , where $P_{ext,1}$ is the pressure per particle exerted by the wall. Add up all of these contributions over particles ( $\bm{n}$ outward-direct, origin at box center), and time average over a very long time, $\langle f\rangle={1\over T}\int_0^T f(t) \, dt$

(3) $\begin{eqnarray*}\sum_j\mathbf{F}_{j,ext}\cdot\mathbf{r}_j&=&\sum_{j \, on \, wall} -P_{ext,1}A_{wall} \mathbf{n}\cdot \mathbf{r}_{j,wall}\nonumber\\ &=&-N_{wall}(t) P_{ext,1}A_{wall} \cdot 6 \cdot(L/2)\nonumber\\ &=&-3 N_{wall}(t) \, P_{ext,1}V\nonumber\\ \langle \sum_j\mathbf{F}_{j,ext}\cdot\mathbf{r}_j\rangle&=& -\langle N_{wall}(t)P_1\rangle V\nonumber\\ &=& -3P_{ext,T} \, Vol\nonumber\end{eqnarray*}$

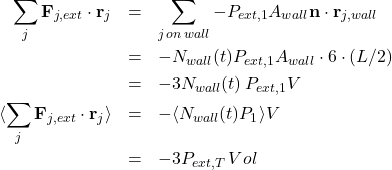
So what is this used for?
In molecular dynamics one keeps track of particle positions and momenta, so the virial theorem can be used to compute pressures. The virial hypothesis is that because any particle in a system confined by walls or interparticle forces will sample a very large phase space (set of $\bm{r}, \bm{p}$ values) over time

${1\over T}\int_0^T\dot{Q} \, dt=0, \qquad 2 \, T-\nu V-3P_{ext,total} \, Vol=0$

In a system confined only by interparticle forces we have

$0=2\langle T\rangle-\nu\langle V\rangle$

Qualifier problems for circular orbits in central potentials, since for such cases

$\langle T\rangle=T={\nu\over 2}\langle V\rangle={\nu\over 2} V, \qquad E=T+V={2+\nu\over 2}V$

As I mentioned above, the averages here can be time averages, or position averages

$\langle X\rangle=\lim_{N\rightarrow \infty} {1\over N}\sum_{i}^N X(t_i), \qquad \langle X\rangle=\lim_{N\rightarrow \infty} {1\over N}\sum_{i}^N X(\bm{r}_i)$

Dynamics (711) We will use such averages quite frequently to separate secular (oscillatory) and nonsecular (accumulating) perturbations by averaging over a period (or by averaging over eccentric anomaly values)

$\langle X\rangle={1\over T}\int_0^T X(t)\, dt={1\over \omega T}\int_0^{2\pi}X(\psi)\cdot (1-\epsilon\cos\psi)\, d\psi$

$={1\over 2\pi}\int_0^{2\pi}X(\psi)\cdot (1-\epsilon\cos\psi)\, d\psi$

Statistical mechanics (715)
The virial theorem says that for $V(|r_j-r_k|)=a|r_j-r_k|^\nu$

$0=2\langle KE\rangle -\nu\langle PE\rangle -3P_{ext}V$

and for a freely gravitating system $P_{ext}=0$ and $\nu=-1$ .
Assemble a ball of constant density $\rho$ matter by bringing in a new layer of thickness $dr$ from infinity where the gravitational potential vanishes; an external agent moving the masses will do work

$dW_{ext}=-dm\Big(-{M(r)G\over r}-0\Big)=-(4\pi \rho r^2 dr)\Big({4\pi r^3\rho G\over 3r}\Big)$

$W_{ext}={(4\pi \rho)^2 GR^5\over 15}={3\over 5}{M^2G\over R}$

and in a closed system this plus the work done by the gravitational field add up to zero.
Consider the work done by the gravitational field as a Hamiltonian potential $PE=V=-{3\over 5}{M^2G\over R}$
and treat the dust/gas to be ideal and nonrelativistic, and we have no external pressure applied, it is self-gravitating.

$0=\langle\dot{Q}\rangle=\langle\sum_j\mathbf{F}_{j,int}\cdot \mathbf{r}_j\rangle+\langle\sum_j\mathbf{p}_{j}\cdot \dot{\mathbf{r}}_j\rangle$

$0=-\langle\sum_j\gbf{\nabla}_j\mathbf{H}\cdot \mathbf{r}_j\rangle+\langle\sum_j\mathbf{p}_{j}\cdot \dot{\mathbf{r}}_j\rangle$

$0=-\langle R{\partial H\over \partial R}\rangle+2\langle KE\rangle, \qquad 3kT=\langle R{\partial H\over \partial R}\rangle={3\over 5}{M^2G\over R}$

Because $\nu=-1$

$2\langle KE\rangle-(-1)\langle PE\rangle=0, \qquad 3kT-{3\over 5}{M^2G\over R}=0$

As $R$ shrinks, $T$ goes up, which is sensible for a collapsing cloud, but the total energy decreases

$2\langle KE\rangle-(-1)\langle PE\rangle=0$

$\langle E\rangle=\langle KE\rangle+\langle PE\rangle={3\over 2\cdot 5}{M^2G\over R}-{3\over 5}{M^2G\over R}=-{3\over 2\cdot 5}{M^2G\over R}$

and therefore a freely gravitating mass of matter has a negative specific heat. It cannot be placed in thermal equailibrium with any system that has positive specific heat.

Home 2.0

Physics 7XX: The virial theorem

Related Posts

Physics 7XX: The virial theorem

Published by Jeff on October 13, 2021October 13, 2021

Related Posts

Protected: GRE-prep: Chemical potential problems

Protected: GRE-prep: Partition function examples

Protected: GRE-prep:Fields from sources