Physics 7xx: Cosmic inflation-I

During the first spring of the pandemic I was teaching 715. A student in the class asked “in an inflation model in which the inflaton $\phi$ tunnels from a false (local) ground state to a true global ground-state, and so $\phi$ jumps from one value (let’s presume it was $\phi=0$ ) to a nonzero value $\phi=v$ , how does the latent heat result in particle creation?”. Asking a question such as this very often stimulates the creation of a homework problem (and of course that’s exactly what happened) in which students can answer the question themselves after carrying out all of the steps.
Let’s present that problem here, and use it as an excuse to have a look at inflation. We will do this in stages, this first post at a survey/introductory 200-level, the next at the 711 level, and the last ala’ 715.

The following is an honors section lecture that I made for Physics 208, a nice gentle starting point. Some details have been “softened”, I hope not to the point where they are incorrectly representd. If that is the case, I hope that you will let me know.

There is a large body of observational evidence that the universe is expanding ala’ the big bang model. The core of hot big-bang cosmology is the
Cosmological principle; the universe looks the same in all directions to all observers (it is isotropic).
We seek an isotropic, expanding solution to Einstein’s field equations in general relativity. Field equation solutions are geometries for spacetime; the physical distance $D$ between events $e_1=(t_1,\bm{r}_1)$ and $e_2=(t_2,\bm{r}_2)$ in the resulting solution is

$D=\int_{e_1}^{e_2}ds, \qquad ds^2=-dt^2+a^2(t)\Big({dr^2\over 1-kr^2}+r^2 d\Omega^2\Big)$

( $k$ is the curvature of spacetime, $a(t)$ is an expansion factor). Look at two simultaneous events $dt=0$ a coordinate distance $dr$ apart; at different times in the life of the universe they are getting physically farther apart

$ds^2=a^2(t) \, dr^2, \quad s=a(t) \, r, \qquad {ds\over dt}=v_s ={da\over dt}\, r=\dot{a} \, r=\tfrac{\dot{a}}{a}\, s\equiv H\, s$

Hubble’s law
This expansion or motion of every coordinate point in the universe away from every other coordinate point is known as Hubble’s law. Hubble’s law says that the velocity with which every point in space recedes from any other point selected as an origin is

$v_s=H(t) \, s, \qquad \mbox{or} \qquad \tfrac{v_s}{s}=H(t)$

where $H(t)$ is the same everywhere in space but may be changing over time. It is measured to be around $500 km/s/Mpc$ . The fact of this expansion has been observationaly verified many times by studying Doppler shifts of distant stars. Hydrogen gas emits light of known wavelengths $\lambda_{rest}$ from the stars, it is received on earth as $\lambda_{rec}$ with a Doppler shift

$\tfrac{\lambda_{rec}-\lambda_{test}}{\lambda_{rest}}=\tfrac{v_s}{c}$

and we know how far away $s$ the stars are since we know their type (absolute magnitude $m$ ) and can measure their apparent magnitude $M_v$

$M_v=m-2.5\log_{10}((\tfrac{s}{10})^2), \quad s=(10 \, pc)\, 10^{(m-M_v)/5}$

Suppose that we lived in a two-dimensional universe in which everything existed on the surface of a sphere of radius $R$ . Galaxies $a,b$ are $s=R\theta$ apart. Galaxies $a,c$ are $s'=R(2\theta)$ apart. Suppose that the sphere radius (“volume” of the universe is $4\pi R^2$ ) is increasing at rate ${dR/dt}=\dot{R}$ . Then galaxy $a$ moves away from galaxy $b$ at speed $v_s=\dot{R}\theta$ , $a$ moves away from galaxy $c$ at speed $v'_s=\dot{R}(2\theta)$ , so divide

${v'_s\over v_s}={s'\over s}, \quad {v'_s\over s'}={v_s\over s}=H$

Hot Big Bang
General relativity connects the density of energy in the universe to the geometry of space-time, in other words the formula for distances in space-time

$ds^2=-dt^2+a^2(t)\Big({dr^2\over 1-kr^2}+r^2 d\Omega^2\Big)$

is the result of a particular distribution of energy, assumed isotropic by the cosmological principle. Let $E/V=\rho c^2$ (we use units with $c=1$ ), let the pressure exerted by all forms of energy be $p$ . The forms of energy are those of matter, radiation, and dark energy

$\rho=\rho_m+\rho_{rad}+\rho_\Lambda$

The first law of thermodynamics tells us about how these energy densities will change as the universe expands

$\rho\sim \left\{\begin{array}{ll} a^{-3}& \mbox{matter}\\ a^{-4} & \mbox{radiation}\\ a^{0} & \mbox{dark energy}\end{array}\right.$

and general relativity then tells us what $H=\tfrac{\dot{a}}{a}$ will be for a universe dominated by each of these:

$H^2={8\pi \over 3m_{P}^2}\rho -{k\over a^2}, \qquad H=\dot{a}/a, \qquad m_P=\sqrt{\tfrac{\hbar c}{G}} \sim 2.176\times 10^{-8} kg$

$k$ is the curvature of space-time, and observations have recently suggested that this is very small, essentially zero. This is one of Einstein’s field equations for our cosmological model geometry $ds^2$ .
As the universe evolves, HBB theory provides two scales; Hubble time $H^{-1}={dt\over d\ln a}$ giving the timescale for evolution of $a(t)$ , and curvature scale $a|k|^{-1/2}$ giving distance scale up to which space can be taken to be flat. The ratio tells us about the energy density versus a critical value (for which expansion would eventually stop, slowed by gravity);

$H^2={8\pi \over 3m_{P}^2}\rho -{k\over a^2}={\rho\over \rho_c} -{k\over a^2}=\Omega H^2-{k\over a^2}, \qquad \sqrt{|\Omega-1|}={H^{-1}\over a|k|^{-1/2}}$

Space is flat if $k=0$ , for fixed $H$ this means the density (which we talked about in an earlier honors lecture) equals the critical value $\rho_c(t)={3m_{P}^2H^2\over 8\pi}\approx 1.8\times 10^{-29}{g\over cm^3}$ presently.

Why inflation?
$\bullet$ Hot big bang deficiencies. Flatness problem.
According to HBB theory, by $1 \, sec$ after the BB light nuclei could have formed, after $10^4$ years matter and radiation densities were about equal, after about $10^5$ years radiation and matter decouple and the CMB is formed, $10^{10}$ years after the BB is today.
Flatness problem. Our HBB equations say

$|\tfrac{\rho}{\rho_c}-1|=|\Omega-1|={|k|\over a^2H^2}$

and BB suggests $\dot{a}=aH$ {\bf decreases} ( $\ddot{a}<0$ ) so $\Omega$ {\bf departs from one over time}.
Today $\Omega$ is $0.1\le \Omega\le 10$ , so extrapolating back to $1 \, sec$ post-BB we would find $|\Omega-1|<10^{-16}$ at that time (really close to one), so no reasonable choice of initial energy density leads to what we see in the universe today; the observed universe is flatter than what HBB evolution predicts from any reasonable initial state. The range $\rho_c<\rho_{init}<\rho_c(1+1\times 10^{-16})$ in order to account for what we see today is just too finely-tuned to be probable.
Caveat. Not all physicists are bothered by fine-tuning issues, which have also been used as a justification for supersymmetry. I see nothing wrong with having some natural parameters needing to be finely tuned.
$\bullet$ CMB uniformity and horizon problem.
From https://wmap.gsfc.nasa.gov we have this map of “13.77 billion year old temperature fluctuations (shown as color differences) that correspond to the seeds that grew to become the galaxies. The signal from the our Galaxy was subtracted using the multi-frequency data. This image shows a temperature range of $\pm 200$ microKelvin”.
Evolution of stars and galaxies (ordered things) from such an extremely uniform (amorphous) distribution of energy is in violation of the second law of thermodynamics (the universe should evolve towards uniformity/structurelessness, not from this to structure such as stars and galaxies. Keep in mind the CMB shows the universe as it was, not as it is.

$\bullet$ Horizon problem. The map above is panoramic; look in any direction (even in opposite directions) and you see a CMB (snapshot of the early universe) that looks the same, very uniform, no matter which way you look. This suggests that all parts of the early universe would have equilibrated with one another. But the CMB was released (according to HBB) about $450,000$ years after the BB, and it would have been about $100\times 10^6$ light years across at the time, and in $450,000$ years heat could not have traveled even one percent of that distance, so equilibrium could not have been reached by that time.
Because we can only see everything up to a horizon (we see now that which occurred a time $t=r/c$ ago a distance $r$ away or less), only those events occurring within the horizon could influence us today. There are parts of the universe that could not have equilibrated because they were not causally linked by the time the the apparent equilibrium was reached.
Caveat. All three of these motivations for inflationary models are seen as non-issues by a significant cross-section of physicists. They may not be problems at all, or may have much simpler more mundane resolutions.
Inflationary model

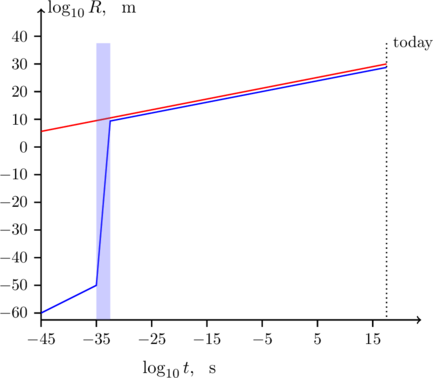
The standard model of particle physics plus HBB (red) predicts an expansion of the universe that does not describe what we see. Cosmic inflation is a modification of the HBB theory that suggests a very rapid and rapidly accelerating expansion of space-time between $10^{-35}$ and $10^{-33}$ seconds after the BB, during which spacetime expanded very much faster than the speed of light. This blew up the radius of the universe by a factor $10^{26}$ during a very short time. No problems with relativity, since no energy actually traveled this fast.

This scenario solves some of the problems with HBB theory.
$\bullet$ The flatness problem. The universe appears to be flat simply because it is actually much bigger than we think it is (one calculation suggests it is $10^{23}$ times the size of the observable universe).
$\bullet$ The horizon problem. The expansion of the universe was so fast during the inflationary era that the initially homogeneous universe that gave rise to the CMB did not have time to get scrambled before it was flung far and wide, so the uniformity was never disrupted, and here is no need for it to have equilibrated through any causal contact.
$\bullet$ The “Monopole/artifact problem”. The standard model predicts that early universe conditions would have produced exotic forms of matter and field configurations that would have proliferated through gravitational forces. We don’t see these today. Inflation says that they have become very diluted and their proliferation was disrupted, which is why we don’t see them. Of course it is equally likely that any theory that predicts the existence of such “artifacts” is simply wrong, or incomplete, which is why we do not see them…

Inflationary models tell us the universe could be very big

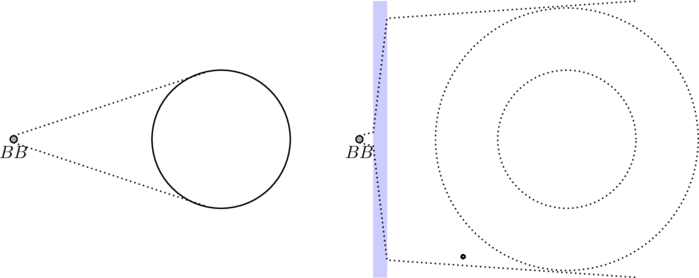
If the universe expanded at $c$ , we would be able to see everything it it today since the outer reaches would be our horizon. In an inflationary scenario much of the universe is outside of our horizon and we can’t see it yet. In both pictures we are at the center of the circle.

Slow-role inflation
What would cause inflation? The idea is that some field (called the inflaton) is providing a negative vacuum energy, or a positive vacuum pressure.
Hot BB says $aH$ always decreases (in other words $\tfrac{1}{Ha}$ always increases), so $|\Omega-1|={|k|\over (aH)^2}$ grows. Reverse this scenario and cause inflation; the acceleration of the expansion is given by

$\ddot{a}/a=-{4\pi\over 3m_{P}^2}(\rho+3p)=-{4\pi G\over 3}(\rho+3p)+{\Lambda\over 3}$

$\Lambda$ is Einstein’s cosmological constant, if we think that this is zero, then

$\ddot{a}=0\quad\mbox{equivalently}\quad {d(H^{-1}/a)\over dt}<0 \quad \mbox{equivalently}\quad p<-{\rho\over 3}$

Effective energy density and pressure of a scalar field by comparison in a universe obeying the cosmological principle will have kinetic $\tfrac{1}{2}\dot{\phi}^2$ and potential energy $V(\phi)$ terms for which (recall $c=1$ )

$\rho={1\over 2}\dot{\phi}^2+V(\phi), \qquad p= {1\over 2}\dot{\phi}^2-V(\phi)$

Insert $\rho,p$ into $k=0$ (because once inflation begins $k$ becomes small) versions of the Friedmann (cosmological) equations (which we will work out in a subsequent post)

$H^2={8\pi \over 3m_{P}^2}\rho -{k\over a^2}, \qquad H=\dot{a}/a, \qquad \dot{\rho}+3H(\rho+p)=0$

$H^2={8\pi \over 3m_{P}^2}({1\over 2}\dot{\phi}^2+V(\phi)), \quad \dot{\phi}\ddot{\phi}-V'(\phi)\dot{\phi}+3H(\dot{\phi}^2)=0$

In inflation $\ddot{a}>0$ or $p<-\rho/3$ synonymously which now implies

${3\over 2}\dot{\phi}^2-3V<-\Big({1\over 2}\dot{\phi}^2+V\Big), \quad \dot{\phi}^2<V$

so inflation occurs when the potential dominates. Think of the field evolution in mechanical terms, the field is a marble rolling back and forth on a potential curve through an equilibrium where inflation stops. One needs the rolling to be slow since $\dot{\phi}^2<V(\phi)$ so the potential must be slowly varying in $\phi$ . What are the candidates for the inflaton $\phi$ ? Perhaps the Higgs field, or something as of yet undetected.

The idea is that some initial quantum fluctuation has given $\phi$ some elevated potential energy $V(\phi)$ , and now the field configuration “slow-rolls” down the potential hill, gaining kinetic energy $\tfrac{1}{2}\dot{\phi}^2$ . Inflation continues while $\dot{\phi}^2<V$ , and stops when we reach a mechanical equilibrium. This “slow-roll” is synonymous with inflation, which is synonymous with accelerated expansion $\ddot{a}>0$ , synonymous with $p<-\tfrac{\rho}{3}$ synonymous with $\tfrac{d(H^{-1}/a)}{dt}<0$ . For example with the field potential

$V(\phi)=V_0e^{-\sqrt{{16\pi\over p}} {\phi\over m_P}}$

which gives rise to power law inflation $a\sim t^p$ , $p>1$ , in units in which $c=1$ , so

$\dot{a}\sim p t^{p-1}, \quad \dot{a}/a=p/t\, \quad p>1$

can be bigger than $1$ , and $\ddot{a}=p(p-1)/t^2>0$ which could be tremendous for small $t$ .

Original Guth model

The field starts out in a local minimum and quantum mechanically tunnels into a global minimum. During the tunneling there is inflation. Inflation stops when the global vacuum (lowest $V$ ) is reached, and the latent heat is released (first order transition) which goes into the formation of an enormous amount of ordinary matter (other particles).
Problem: too much inflation occurs and the universe is left too empty (“graceful exit” problem). Bubbles (parallel universes causally disconnected from our own) form, experience negative pressure, and rapidly expand and coalesce. Attempts are made to fine-tune the bubble formation. The problem here seems to be the very rapid decay from false to global vacuum, and inflation may never end.
An inflationary model that can exit gracefully

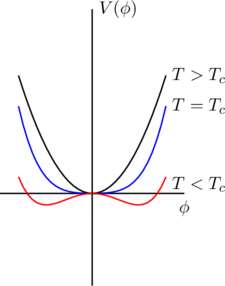
Linde-Steinhardt-Albrecht solution to “gracefule exit” (how to get out of endless inflation) is to allow slow evolution/roll of the inflaton field while the universe cools until a critical temperature is reached, then the field settles into a global minimum in a second order phase transition that does not require tunneling.

Home 2.0

Physics 7xx: Cosmic inflation-I

Related Posts

Physics 7xx: Cosmic inflation-I

Published by Jeff on November 21, 2021November 21, 2021

Related Posts

Protected: GRE-prep: Circuits

Protected: GRE-prep: QM spin problems

Protected: GRE-prep, Phys 415: maximal entropy principle