Physics 7xx: Cosmic inflation-III, electric boogaloo

The sequel that no-one asked for: “in an inflation model in which the inflaton $\phi$ tunnels from a false (local) ground state to a true global groundstate, and so $\phi$ jumps from one value (let’s presume it was $\phi=0$ ) to a nonzero value $\phi=v$ , how does the latent heat result in particle creation?”

As I previously said, this was a question raised in 715, and it led to the write-up of this homework problem that guides you to the answer. It draws heavily from the Physics 711 discussion of normal modes with dissipation, illustrating why we require classical mechanics and why we cover normal modes (TL:DR, to solve modern problems you need to know the basics, even if they are “classics”). It also draws upon ideas from 831 (or 535/735) used to describe fundamental processes such as particle decay and creation.

Let us assume that the inflaton $\phi$ is coupled to other fields, call $\chi$ such a (matter) field, taken to be scalar for simpicity, so that if you have taken 831 you could solve this problem. Latent heat is the energy given off in this transition. We further assume that the mechanism of particle creation (reheating) is simply that the energy stored in the inflaton field is transferred into the matter fields. You will therefore compute the energy loss of the inflaton field during its post-inflation evolution. You will take this evolution to be an oscillation about its new ground state, damped because of particle ( $\chi$ ) creation. Prerequisites are a basic understanding of slow-roll inflation, and sections 11 and 25 of Srednicki’s QFT text, or the corresponding chapters in some alternative.

We take as the Lagrangian density

$\mathcal{L}=-\tfrac{1}{2}(\partial_\mu\phi)^2-V(\phi)-\tfrac{1}{2}(\partial_\mu\chi)^2-\tfrac{1}{2}m_\chi^2\chi^2-\tfrac{1}{2}\xi\chi^2 R-\tfrac{1}{2}g^2\phi^2\chi^2-g^2 v \phi\chi^2$

$V(\phi)=\tfrac{1}{2}m^2\phi^2+\mathcal{O}(\phi^4)$

in which $g, \xi$ are small, $v$ is the inflaton vacuum expectation value since we have done $\phi-v\rightarrow\phi$ so that $\phi=0$ is the minimum of $V$ ( $V(\phi)=\tfrac{1}{2}m^2\phi^2+\cdots$ ) and $m$ is the inflaton mass at the potential minimum $m\sim 10^{13} GeV$ . $\phi$ and $\chi$ are real scalar fields. $R$ is the Ricci scalar for the Friedmann spacetime, which we worked out in the second installment. You can see that this model allows for gravitational particle creation too.
The end of inflation occurs when $H\sim m$ , so that the rate of expansion falls off as $H\sim 1/t< m$ .

Part A.
First we (I mean you) calculate the decay rate of the inflaton at the tree-level according to the simplest part of our Lagrangian density

$\mathcal{L}'=-\tfrac{1}{2}(\partial_\mu\phi)^2-\tfrac{1}{2}m^2\phi^2-\tfrac{1}{2}(\partial_\mu\chi)^2-\tfrac{1}{2}m_\chi^2\chi^2+\tfrac{1}{2}h \phi\chi^2$

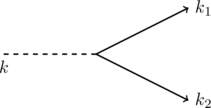
which allows $\phi\rightarrow \chi\chi$ if $m_\phi>2m_\chi$ with the illustrated graph, which has matrix element $\mathcal{T}=h=2g^2 v$ (tree level) if $h$ is the exact vertex for all three particles on shell. Note that the outgoing particles are identical. Read Ch. 11 of Srednicki. You will observe that we have a $\phi$ decay rate

$d\Gamma={1\over 2m_\phi} dLIPS_2 |\mathcal{T}|^2={1\over 2m_\phi}(2\pi)^4 \delta^4(k_1+k_2-k) \tilde{dk}_1 \tilde{dk}_2 |\mathcal{T}|^2$

$\tilde{dk}={d^3 k\over (2\pi)^3 2\omega}$

Evaluate this in the CM frame and show that if $m_\phi=m>>m_\chi$ then $\Gamma_\phi\approx {g^4v^2\over 8\pi m}$ .

Solution
$dLIPS_2$ is differential Lorentz invariant phase space for two bodies. We have a symmetry factor of $2$ for identical outgoing particles, from Srednicki Eqtn-11.30, evaluated in the rest frame of the inflaton, incorporating $S$

$dLIPS_2={|\bm{k}_1|\over 16\pi^2\sqrt{s}}d\Omega, \quad |\bm{k}_1|=|\bm{k}_2|={1\over 2}(m_\phi^2-4m_\chi^2)^{1/2}$

$\Gamma={S\over 2}{1\over 2m_\phi}h^2 (m_\phi^2-4m_\chi^2)^{1/2}{4\pi\over 16\pi^2 \sqrt{s}}\approx {g^4v^2\over 8\pi m_\phi}$

Part B.
Next you must obtain some equations describing the slow-roll chaotic inflation model for a simple scalar inflaton field $\phi$ . In a homogeneous universe a scalar field is a function of just time. For a perfect fluid the stress-momentum tensor is

$T^{ab}=(\rho+p/c^2)u^au^b+pg^{ab}, \qquad u^au^bg_{ab}=c^2, \quad T^{ab}=\left(\begin{array}{cccc} \rho & 0 & 0 & 0\\ 0 & p & 0 & 0\\ 0 & 0 & p & 0 \\ 0 & 0 & 0 & p\end{array}\right)$

$g_{ab}=\left(\begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1\end{array}\right)$

(the same signature that I used in 711, and the opposite of the choice made in the previous post, I will go back and change that one…). For a scalar field the stress-momentum tensor is

$T^a_b={\partial \mathcal{L}\over \partial (\partial_a\phi)}\partial_b\phi-\delta^a_b \mathcal{L}$

$\mathcal{L}={1\over 2}\partial_a\phi\partial^a\phi-V(\phi)$

Show that if we interpret the fluid energy density and pressure to come from $\phi$ , then

$\rho={1\over 2}\dot{\phi}^2+V(\phi), \qquad p= {1\over 2}\dot{\phi}^2-V(\phi)$

Solution
OK, using ideas from the field theory part of 711 or alternatively 735 or 831, for a scalar field

$T^a_b=\partial^a\phi\partial_b\phi-\delta^a_b({1\over 2}\partial_c\phi\partial^c\phi-V(\phi))$

$T^{ab}=\partial^a\phi\partial^b\phi-g^{ab}({1\over 2}\partial_c\phi\partial^c\phi-V(\phi))$

compare with the fluid

$\rho=T^{00}=\dot{\phi}^2-({1\over 2}\dot{\phi}^2-V(\phi))={1\over 2}\dot{\phi}^2+V(\phi)$

$p=T^{11}=0+({1\over 2}\dot{\phi}^2-V(\phi))={1\over 2}\dot{\phi}^2-V(\phi)$

Part C.
Now you must incorporate this into a description of the expansion of the universe. Let us assume a flat, expanding, isotropic universe

$ds^2=dt^2-a^2(t)\Big(dr^2+r^2d\Omega^2\Big)$

For this metric, the Einstein field equations have $00$ component and trace equivalent to (the Friedmann equations)

${\dot{a}^2\over a^2}={8\pi G\rho\over 3}, \qquad {\ddot{a}\over a}=-{4\pi G\over 3}\Big(\rho+3p/c^2\Big)$

but you will set $c=1$ . You should show this, but let’s let that be optional. Solve the first Friedmann equation for a matter-dominated universe (one for which $\rho$ is given by the matter energy density $\rho(t)=\rho_0/a^3$ ). How does $a$ vary with time for such an epoch (an old qualifier question)? Show that for your solution $\ddot{a}<0$ .

What is inflation? It is $\ddot{a}>0$ . This is synonymous with $p< -{\rho c^2\over 3}$ . Therefore the solution that you found in the previous part is a post-inflation simple expanding universe solution, which is what we need for the reheat problem. Show that the Friedmann equations imply that

$\dot{\rho}=-3H\Big(\rho+p\Big)\quad \mbox{in which}\quad H(t)={\dot{a}\over a}$

Next insert your energy density and pressure due to the inflaton field into these equations to obtain an equation of evolution for $\phi$ .

Solution
We did this stuff in the previous post on inflation, now we combine those results with the scalar field bits from above:

${\dot{a}^2\over a^2}={8\pi G\rho_0\over 3a^3}, \quad \sqrt{a}da=\sqrt{{8\pi G \rho_0\over 3}}\, dt,$

$a(t)=\Big({3\over 2}\sqrt{{8\pi G \rho_0\over 3}}\, t\Big)^{2/3}, \quad a\sim t^{2/3}$

Next we reduce

${3\over 8\pi G}\Big(2{\ddot{a}\dot{a}\over a^2}-2{\dot{a}^3\over a^3}\Big)={3\over 4\pi G}H\Big(-{4\pi G\over 3}\Big(\rho+3p/c^2\Big)-{8\pi G\rho\over 3}\Big)=\dot{\rho}$

down to

$\dot{\rho}+3H(\rho+p)=0$

and put $\rho(\phi)$ into

$H^2={8\pi \over 3m_{P}^2}\rho, \qquad H=\dot{a}/a={2\over 3t}$

$H^2={8\pi \over 3m_{P}^2}({1\over 2}\dot{\phi}^2+V(\phi))$

and put $\rho(\phi)$ and $p(\phi)$ into $\dot{\rho}+3H(\rho+p)=0$ :

$\dot{\phi}\ddot{\phi}+V'(\phi)\dot{\phi}+3H(\dot{\phi}^2)=0, \qquad \ddot{\phi}+V'(\phi)+3H\dot{\phi}=0$

Part D.
Let $V(\phi)=\tfrac{1}{2}m^2\phi^2+\mathcal{O}(\phi^4)$ and
obtain this equation for inflaton post inflation evolution:

$\ddot{\phi}+3H(t) \dot{\phi}+m^2\phi\approx 0$

in which you are neglecting higher order terms in $V$ since after inflation, with $\phi$ shifted by $v$ , the inflaton field is small. Now show that there is a solution (assuming that during the reheating/post inflation (that means $\ddot{a}\le 0$ ) phase, $m>>H$ so $\Phi(t)$ changes very slowly) that looks like

$\phi(t)\approx \Phi(t)\sin (m t)$

Finally, produce an argument for the conclusion that $\Phi\sim a^{-3/2}\sim t^{-1}$ . Hint: in a matter-dominated universe post-inflation, explain why $\rho c^2\propto a^{-3}$ , then consider time-averaged $\rho$ and $p$ .

Solution
Factoring $\dot{\phi}\ne 0$ from the results of part C gives us this EOM.
This is a very underdamped oscillator, for which a solution exists for the requested form for a constant $H$

$\phi=e^{-3H t}\Big(\phi_0 \cos(\sqrt{m^2-9H^2} t)+{m\Phi_0+3H\phi_0\over \sqrt{m^2-9H^2}}\sin(\sqrt{m^2-9H^2} t)\Big)$

and so at least an approximate solution should exist for $H$ not constant, of the form

$\approx \Phi(t) \, \sin(mt)$

For matter dominated we have $3H=2/t$ and the equation of motion becomes

$\ddot{\phi}+{2\over t}\dot{\phi}+m^2\phi$

which is a spherical Bessel equation with solution $\phi=j_0(mt)=\sqrt{{\pi\over 2t}}J_{1/2}(mt)={\sin(mt)\over mt}$ which is precisely of the suggested form. Discarding terms of order $1/t^2$ then

$\langle \rho\rangle=\tfrac{1}{2}\langle \dot{\phi}^2\rangle+\tfrac{1}{2}m^2\langle\phi^2\rangle\approx \tfrac{1}{2}m^2\Phi^2(t)\Big(\langle \cos^2(mt)\rangle+\langle \sin^2(mt)\rangle\Big)\approx\tfrac{1}{2}m^2\Phi^2(t)$

$\langle p\rangle=\tfrac{1}{2}\langle \dot{\phi}^2\rangle-\tfrac{1}{2}m^2\langle\phi^2\rangle\approx\tfrac{1}{2}m^2\Phi^2(t)\Big(\langle \cos^2(mt)\rangle-\langle \sin^2(mt)\rangle\Big)\approx 0$

For a matter-dominated universe $\rho\sim m/V$ and $V\sim a^3$ ( $c=1$ )

$\rho=\tfrac{1}{2}m^2\Phi^2\sim a^{-3}, \qquad \implies\qquad \Phi\sim a^{-3/2}\sim t^{-1}$

which agrees with the exact solution (phew).

Part E.
Next we try to get a handle on how particle creation affects post-inflation (oscillatory stage) evolution of the inflaton field. This can be accounted for by including in the equation of motion, the denominator of the QFT propagator for $\phi$

$\ddot{\phi}+3H(t) \dot{\phi}+(m^2+\Pi(\omega))\phi=0$

in which $\Pi(\omega)$ is the Minkowski space polarization operator for $\phi$ . Carefully read section 25 of Srednicki and convince yourself of the connection between the on-shell $\Phi$ function and the decay rate $\Gamma_\phi$
to show that the inflaton evolves post inflation (during oscillations) as

$\ddot{\phi}+3H(t) \dot{\phi}+m^2\phi+\Gamma_\phi\dot{\phi}\approx 0$

and so the decay rate acts like friction, damping oscillations.
Show that the solution is

$\phi=\Phi_0 e^{-\tfrac{1}{2}(\int 3H\, dt-\Gamma_\phi t)}\sin(m t)=\Phi_0 t^{-1}e^{-\tfrac{1}{2}\Gamma_\phi t}\sin(m t)$

using $H={2\over 3t}$ apropos of a matter-dominated expansion epoch.
Show that during particle production

${d\over dt}(\rho_\phi a^3)=-\Gamma_\phi \rho_\phi a^3, \qquad {d\over dt}(n_\phi a^3)=-\Gamma_\phi n_\phi a^3$

You have shown that after the inflation ceases and the inflaton field} evolves by simply oscillating about the new global minimum, it decays by losing energy to particle creation, into whatever fields are coupled to it. It may be a simplistic point of view but this offers us an interpretation of the mechanism of the latent heat produced in the transition.

Solution This is the punchline: Eqtn. 25.24 of Srednicki (one-loop corrections to the inflaton propagator)

$Im \Pi(-m^2)=m\Gamma_\phi, \quad\mbox{so that}\quad \ddot{\phi}+3H(t) \dot{\phi}+(m^2+im\Gamma_\phi)\phi=0$

so oscillatory solutions $\phi\sim e^{im t}$ will be described by

$\ddot{\phi}+3H(t) \dot{\phi}+m^2\phi+\Gamma_\phi\dot{\phi}\approx 0$

This is (further) damped oscillator, energy loss of the inflaton field is seen to be directly due to $\chi\chi$ (matter) creation, a mechanism for the latent heat creation. Similar arguments using the exact propagator are used in Itzykson and Zuber to compute fermion pair creation rates by constant electric fields,

For the rest,

${d\over dt}(\rho a^3)=\dot{\rho}a^3+3\rho a^2\dot{a}=\dot{\phi}a^3(\ddot{\phi}+m^2\phi+3H\dot{\phi})$

if we use $\rho\rightarrow \langle \rho\rangle=\langle \dot{\phi}^2\rangle$ , since $\langle \dot{\phi}^2\rangle=\langle m^2\phi^2\rangle$
then (and $\rho_\phi\sim m_\phi c^2 n_\phi$ where $n$ is particle density)