Physics 711 to 831: The road to the path integral

Published by Jeff on December 4, 2021December 4, 2021
Jeff

Physics 711 to 831: The road to the path integral

First some Physics 711. Recall that in Hamiltonian formalism

    \[\dot{q}=\Big({\partial H\over \partial p}\Big)_q=\{q,H\}_{pb}, \qquad \dot{p}=-\Big({\partial H\over \partial q}\Big)_p=\{p,H\}_{pb}\]

    \[\{A,B\}_{pb}=\Big({\partial A\over \partial q}\Big)_p\Big({\partial B\over \partial p}\Big)_q-\Big({\partial A\over \partial p}\Big)_q\Big({\partial B\over \partial q}\Big)_p \hspace{5cm}\]

which replace the Lagrange-Euler equations

    \[\delta \int_{t_i}^{t_f}L dt=\delta \int_{t_i}^{t_f}\Big(p\dot{q}-H(q,p)\Big) dt=0 \hspace{5cm}\]

and for any F=F(q,p,t)

    \[\dot{F}=\{F,H\}_{pb}+{\partial F\over \partial t}\]

Canonical transformations (q,p)\rightarrow(Q,P) preserve the symplectic structure

    \[\dot{Q}=\Big({\partial K\over \partial P}\Big)_Q \quad \dot{P}=-\Big({\partial K\over \partial Q}\Big)_P\]

    \[ \int_{t_i}^{t_f}\Big(p\dot{q}-H(q,p)\Big) dt= \int_{t_i}^{t_f}\Big(P\dot{Q}-K(Q,P)\Big) dt\]

    \[\quad\implies\quad p\dot{q}-H(q,p)=P\dot{Q}-K(Q,P)+{dF\over dt}\]

and F generates the transformation; if F=F(q,Q)

    \[p=\Big({\partial F\over \partial q}\Big)_Q, \quad P=-\Big({\partial F\over \partial Q}\Big)_q,\quad K=H+{\partial F\over \partial t} \hspace{6cm}\]

For a type-2 transformation F=F(q,P)

    \[p=\Big({\partial F\over \partial q}\Big)_P, \quad Q=\Big({\partial F\over \partial P}\Big)_q \]

There is a nice way to write an infinitismal transformation as a deviation from a unit transformation

    \[F(q,P)=qP+\epsilon F'(q,P), \quad p=P+\epsilon \Big({\partial F'\over \partial q}\Big)_P, \quad Q=q+\epsilon \Big({\partial F'\over \partial P}\Big)_q\]

or

    \[\delta q=Q-q=\{q,\epsilon F'\}_{pb}, \qquad \delta p=P-p=\{p,\epsilon F'\}_{pb}\]

The canonical transformation from (q,p)\rightarrow(Q,P) for which Q,P are constants can be constructed in such a manner that (Q,P) are the {\bf initial data}, which is equivalent to solving the Hamiltonian EOMs. In this case K=K(Q,P) is also a constant, and in 711 we took it to be zero as an expedient, and the type-1 generating function is called S(q,Q,t), the Hamilton-Jacobi function,

    \[K=0=H(q,p)+{\partial S\over \partial t}, \qquad H(q,{\partial S\over \partial q})+{\partial S\over\partial t}=0\]

which we solve for S, and then P=-\Big({\partial S\over \partial Q}\Big)_q can be inverted to get q(Q,P,t). S really is the action integral, since

    \[{dS\over dt}={\partial S\over\partial t}+\Big({\partial S\over\partial q}\Big)_Q\dot{q}+\Big({\partial S\over\partial Q}\Big)_q\dot{Q}={\partial S\over\partial t}+\Big({\partial S\over\partial q}\Big)_Q\dot{q}=-H+p\dot{q}\]

therefore

    \[S=\int_{t_i}^{t_f}\Big(p\dot{q}-H\Big)dt=\int_{t_i}^{t_f}L\, dt\]

Despite the stark beauty of this formalism, nobody ever seems to like it much in 711.
What would this look like in quantum mechanics? The problem was considered by Dirac in 1933 and again by Feynmann in 1948. Unfortunately q is not just a label (like t is) in QM, it becomes an operator, which is the source of some troubles, it also becomes a state-label for the set of states associated with sharp position measurement outcomes

    \[\hat{q}|q\rangle=q|q\rangle, \qquad \langle q|q'\rangle=\delta(q-q'), \qquad \int dq \, |q\rangle\langle q|=1, \qquad \hat{p}|q\rangle={\hbar\over i}{\partial \over \partial q}|q\rangle\]

Consider a quantum canonical transformation (\hat{q},\hat{p})\rightarrow(\hat{Q},\hat{P}) (note that \hat{q} and \hat{Q} probably do not commute) and the mixed matrix element (\hat{q} is hermitian)

    \[\langle q|\hat{q}|Q\rangle=q\langle q|Q\rangle, \qquad \langle q|\hat{Q}|Q\rangle=Q\langle q|Q\rangle\]

    \[\langle q|\hat{p}|Q\rangle=-{\hbar\over i}{\partial \over \partial q}\langle q|Q\rangle, \quad \langle q|\hat{P}|Q\rangle={\hbar\over i}{\partial \over \partial Q}\langle q|Q\rangle\]

(convert to wave-mechanics notation and integrate by parts if you need to).

The problem of constructing a standard basis for operators constructed by phase-space quantization is an old one, considered by Born and Jordan in 1925, who proposed completely symmetric combinations (Weyl ordered)

    \[ T_{0,0}=1, \quad T_{1,0}=\hat{p}, \quad T_{0,1}=\hat{q}, \quad T_{1,1}=\tfrac{1}{2} (\hat{p}\hat{q}+\hat{q}\hat{p})\]

and so on, and McCoy ordering

    \[T_{m,n}={1\over 2^m}\sum_{\ell=0}^m{m\choose\ell} \hat{p}^\ell \hat{q}^n\hat{p}^{m-\ell}\]

which parallels the Poincare’-Birkhoff-Witt ordering of universal enveloping algebras. We run into this question of ordering when we try to compute

    \[\langle q|f(\hat{q},\hat{Q})|Q\rangle\]

so Dirac restricted attention to those functions of the form f(\hat{q},\hat{Q})=f_q(\hat{q})f_Q(\hat{Q}), then

    \[\langle q|f(\hat{q},\hat{Q})|Q\rangle=f(q,Q)\langle q|Q\rangle\]

Dirac then defines the F-function

    \[\langle q|Q\rangle=e^{F(q,Q)/i\hbar}\]

and shows that it is the generator of canonical transformations (type-1) since then

    \[\langle q|\hat{p}|Q\rangle=-{\hbar\over i}{\partial \over \partial q}\langle q|Q\rangle={\partial F\over \partial q}\langle q|Q\rangle, \qquad \langle q|\hat{P}|Q\rangle={\hbar\over i}{\partial \over \partial Q}\langle q|Q\rangle=-{\partial F\over \partial Q}\langle q|Q\rangle\]

if the derivatives {\partial \hat{F}\over \partial \hat{q}} and {\partial \hat{F}\over \partial \hat{Q}} are appropriately ordered (is this even possible? What does this heuristic even mean? Probably this; compute {\partial F\over \partial q} {\bf then} replace q\rightarrow \hat{q}, Q\rightarrow \hat{Q} in the resultant)

    \[{\partial F\over \partial q}\langle q|Q\rangle=\langle q|{\partial \hat{F}\over \partial \hat{q}}|Q\rangle, \qquad \hat{p}={\partial \hat{F}\over \partial \hat{q}}, \qquad \hat{P}=-{\partial \hat{F}\over \partial \hat{Q}}\]

The stage is set for the Feynmann path integral. Now let q=q(t) and Q=q(T).

Then F=S and we can
consider transition amplitudes}or conditional probability densities such as

    \[\langle Q | q\rangle\sim e^{-{i\over \hbar}\int_t^{T}L \, dt}\]

Why? Because with q,Q taken to be independent we know that H(q,{\partial S\over \partial q})=-{\partial S\over \partial t} and P=-\Big({\partial S\over \partial Q}\Big) with P,Q constants of the motion, and

    \[{dS\over dt}={\partial S\over \partial t}+{\partial S\over \partial q}\dot{q}=-H+p\dot{q}=-L\]

Go back to 711 where we showed that the type-2 generating function with F_2(q,P)=qP+\epsilon F(q,P) with F_2=H generates time translation Q=q(t+\epsilon))=q+\epsilon\dot{q}+\cdots and this is a Legendre transformation of a type-1 function F_1(q,Q)=F_2-QP

    \[F_1=qP+\epsilon H-QP=\epsilon\Big(H-P{(Q-q)\over \epsilon}\Big)=\epsilon (H-P\dot{q})=-dt\, L, \quad \epsilon=dt\]

which we can iterate to \langle Q | q\rangle\sim e^{-{i\over \hbar}\int_t^{T}L \, dt} for finite (non-infinitismal) T.

An important thing to note is that the right-hand side contains no operators. As Ramond points out this formula gets us into trouble for finite t-T because in the amplitude \langle q|Q\rangle we can subdivide [t,T] into short intervals and insert complete sets of states, resulting in a {\bf exact} quantum-mechanical formula as an alternative starting point for the iteration, because of course q and therefore L change as t changes

    \[\langle q(T) | q(t)\rangle=\int dq_1\cdots dq_{n-1}\langle q(T)|q_{n-1}\rangle\langle q_{n-1}|q_{n-2}\rangle\cdots\langle q_2|q_1 \rangle\langle q_{1}|q(t)\rangle\]

but writing the right-hand side of the generating function above as a product of factors, one for each sub-interval within [t,T] does not reproduce the integrations needed to make the formula exact. Feynmann observed that if the generating function formula is true for infinitismal times, we are back to our formmula gotten by semi-classical considerations

    \[\langle q(t) | q(t+dt)\rangle=A\, e^{{i\over \hbar}L(q(t),q(t+dt)) \, dt}\]

In his excellent book “Field Theory, a Modern Primer”, P. Ramond observes that L(q(t),q(t+dt)) dt=F(q,Q) as is apropos of HJ theory, we showed where this comes from explicitly above by using the relations between type-1 and 2 generating functions), over this interval then F can be written in terms of \dot{q}=(Q-q)/\epsilon=(Q-q)/dt and q, and since we must integrate over the intermediate states

    \[\langle q(T)|q(t)\rangle=\lim_{N\rightarrow\infty}\prod_{j=1}^{N-1} A \, dq_j \, e^{{i\over \hbar}\int_t^T L(q,\dot{q}) \, dt}\]

and as \hbar\rightarrow 0 the only contribution according to the Riemann-Lebesque theorem will come from the path with stationary action, the classical path.\\
We would say that \langle q(t+dt)|q(t)\rangle represents the amplitude for detection at q'=q(t+dt) at time t+dt given a condition of detection at time t resulted in a value q=q(t). In other words the modulus squared of this item is a conditional probability for particle detection resulting in one value granted that it was previously detected at a specified location.

Let’s do it all (again) systematically from a quantum-mechanical starting point in the Schrodinger picture. The purpose is to obtain the amplitude as a sum over paths. We seek the conditional probability amplitude that if the particle is detected at q' at t' it will be detected at q'' at t''. Since

    \[f(t+dt)=e^{dt \, \partial_t}f(t), \quad \mbox{and} \quad \hat{H}=i\hbar \partial_t\]

we have

    \[\langle q'',dt|q',0\rangle=\langle q''|e^{-i\hat{H} dt/\hbar}|q'\rangle\]

but since in general [\hat{H}(t),\hat{H}(t')]\ne 0 we apply these time-evolutions in order, by subdividing t''-t' into many intervals

(1)   \begin{eqnarray*}\langle q''|T \, e^{-i\int_{t'}^{t''}\hat{H} dt/\hbar}|q'\rangle&=&\langle q''|e^{-i\hat{H}_N dt/\hbar}\cdots e^{-i\hat{H}_j dt/\hbar}\cdots e^{-i\hat{H}_1 dt/\hbar} |q'\rangle\nonumber\\ &=&\int \prod_{j=1}^N dq_j\langle q''|e^{-i\hat{H}_N dt/\hbar}|q_N\rangle\langle q_N|e^{-i\hat{H}_j dt/\hbar}|q_{N-1}\rangle\langle q_{N-1}|\cdots \langle q_1|e^{-i\hat{H}_1 dt/\hbar} |q'\rangle\nonumber\end{eqnarray*}

    \[\mbox{ For}\quad \hat{H}={\hat{p}^2\over 2m} + V(\hat{q}),\qquad e^{-i {dt\over \hbar}({\hat{p}^2\over 2m} + V(\hat{q}))}\ne e^{-i {dt\over \hbar}{\hat{p}^2\over 2m}} \, e^{-i {dt\over \hbar}V(\hat{q})}\]

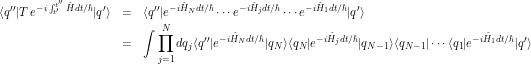
however the Baker-Campbell-Hausdorff formula e^{A+B}=e^A e^B e^{-{1\over 2}[A,B]} allows us to say that

    \[ e^{-i {dt\over \hbar}({\hat{p}^2\over 2m} + V(\hat{q}))} = e^{-i {dt\over \hbar}{\hat{p}^2\over 2m}} \, e^{-i {dt\over \hbar}V(\hat{q})} \, e^{ \mathcal{O}(dt^2)}\]

in which the third term on the right side contains terms generated by the commutator of the kinetic and potential energy operators. We can see that for very short times this last term can be taken to be 1.

Insert a complete set of momentum states into

(2)   \begin{eqnarray*}\langle q" |e^{-dt \,{i\over \hbar}\hat{H}}| q'\rangle&=&\langle q" | e^{-i {dt\over \hbar}{\hat{p}^2\over 2m}} \, e^{-i {dt\over \hbar}V(\hat{q})} \, e^{ \mathcal{O}(dt^2)}| q'\rangle\nonumber\\ &=&\int \, d\ell \, \langle q" | e^{-i {dt\over \hbar}{\hat{p}^2\over 2m}} \, | \ell \rangle\langle \ell| \, e^{-i {dt\over \hbar}V(\hat{q})}| q'\rangle\nonumber\end{eqnarray*}

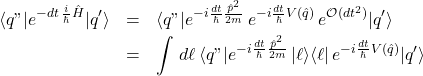
But for the momentum state |\ell\rangle and position state |q\rangle

    \[e^{-i {dt\over \hbar}{\hat{p}^2\over 2m}} \, | \ell \rangle=e^{-i {dt\over \hbar}{\ell^2\over 2m}} \, | \ell \rangle, \qquad e^{-i {dt\over \hbar}V(\hat{q})}| q\rangle=e^{-i {dt\over \hbar}V(q)}| q\rangle\]

in which \ell and q are the eigenvalues of the Hermitean operators \hat{p} and \hat{q} respectively.

We arrive at

(3)   \begin{eqnarray*}\langle q" |e^{-dt \,{i\over \hbar}\hat{H}}| q'\rangle&=&\int \, d\ell \, e^{-i {dt\over \hbar}{\ell^2\over 2m}} \, \langle q" | \ell \rangle\langle \ell| \,q'\rangle e^{-i {dt\over \hbar}V(q')}\nonumber\\ &=&\int \, {d\ell\over 2\pi} \, e^{-i {dt\over \hbar}{\ell^2\over 2m}} \, e^{-i\ell{(q"-q')\over \hbar}} \, e^{i {dt\over \hbar}V(q')}\nonumber\\ &=&\int \, {d\ell\over 2\pi} \, e^{-i {dt\over \hbar}\Big({\ell^2\over 2m}-\ell{(q"-q')\over dt}+V(q')\Big)}\nonumber\\ &=& {1\over \sqrt{-2\pi i dt}}e^{i{dt\over \hbar}({1\over 2}\dot{q}^2-V(q_1))}\nonumber\end{eqnarray*}

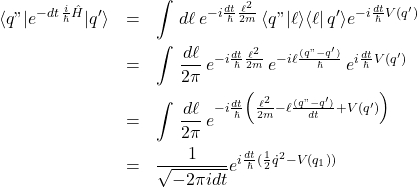
after performing the integral by completing the square. Assemble many such factors by integrating over complete sets of intermediate position states, the result is usually written as\\

    \[\langle q",t" | q',t'\rangle=\int\prod_{j=1}^N dq_j \, {dp_j\over 2\pi}e^{{i\over \hbar}\Big(p_j(q_{j+1}-q_j)-H(p_j,q_j)dt\Big)}=\int \mathcal{D}[q]_{q',q"}\mathcal{D}[p] \, e^{{i\over \hbar}\int_{t'}^{t"} \Big(p(t)\dot{q}(t)-H(q(t),p(t))\Big) dt}\]

In the path integral expression there are two hidden mathematical problem areas. The first is the integration measure function \mathcal{D}[q(t)]. In order that the path integral reproduces the correct free particle green function, this measure must be a complex number. It really should be of no surprise that if the integral is performed by dividing the path into N segments of duration dt={T\over N}, that this measure depends on the number N. The explicit measure (restore the mass) is

    \[ \mathcal{D}[q(t)]= \sqrt{{im\over 2\pi \hbar \, dt}} \prod_{i=1}^N \Big(\sqrt{{im\over 2\pi \hbar \, dt}} \, dq_i\Big)\]

    \[=\Big(\sqrt{{im\over 2\pi \hbar \, dt}}\Big)^{N+1} \prod_{i=1}^N \, dq_i\]

The second issue is the fact that the exponent oscillates. The common means of understanding such integrals (thanks to N. Weiner) is to give dt a vanishing imaginary part in order to justify the use of the Gaussian integration formula in their quadrature. In quantum field theory we refer to this as euclideanization, or a Wick rotation.

Direct evaluation for free particle

    \[\int \big(\sqrt{{im\over 2\pi \hbar \, dt}}\big)^{N+1} \prod_{i=1}^N \, dq_i \, e^{i{m\over 2 \hbar }\big({(q_1-q_0)^2\over dt}+{(q_2-q_1)^2\over dt}+\cdots +{(q_{N}-q_{N-1})^2\over dt}+{(q_f-q_{N})^2\over dt}\big)}\]

The terms within the large parenthesis can be written as

    \[ {im\over 2\hbar \, dt}(q_0^2+q_f^2)+\bm{q}^T\cdot\bm{M}\cdot\bm{q} +\bm{v}^T\cdot\bm{q}\quad\mbox{in which}\quad \bm{q}=(q_1, q_2, q_3, \cdots, q_{N}), \quad \bm{v}={im\over 2\hbar \, dt}(-2 q_0, 0, \cdots, 0, -2 q_f)\] and \[ \bm{M}={im\over 2\hbar \, dt}\left(\begin{array}{ccccccc} 2 & -1 & 0 & \cdots & 0 & 0 & 0\\ -1 & 2 & -1 & 0 & \cdots & 0 & 0 \\ 0 & -1 & 2 & -1 & 0 & \cdots & 0 \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot\\ 0 & \cdots & 0 & -1 & 2 & -1 & 0\\ 0 & 0 & \cdots & 0 & -1 & 2 & -1 \\ 0 & 0 & 0 & \cdots & 0 & -1 & 2 \\ \end{array}\right)\]

    \[\int \big(\sqrt{{im\over 2\pi \hbar \, dt}}\big)^{N+1} \big(\prod_{i=1}^{N}dq_i\big) \, e^{{im\over 2\hbar \, dt}(q_0^2+q_f^2)+\big(\bm{q}^T\cdot\bm{M}\cdot\bm{q} +\bm{v}^T\cdot\bm{q}\big)}\]

If we make an orthogonal transformation \bm{q}=\bm{O}\cdot\bm{y}, \qquad \bm{O}^T\cdot\bm{O}=1 such that the matrix \bm{O} diagonalizes the matrix \bm{M}; \bm{O}^T\cdot\bm{M}\cdot \bm{O}=\bm{\Lambda} then since orthogonal transformations have determinant of one the integration measure is unaffected \prod_{i=1}^{N} dq_i=\det{O}\prod_{i=1}^{N} dy_i=\prod_{i=1}^{N} dy_i the integrations will all become decoupled

(4)   \begin{eqnarray*}\langle q",t" | q',t'\rangle&=& \int \Big(\sqrt{{im\over 2\pi \hbar \, dt}}\Big)^{N+1} \Big(\prod_{i=1}^{N}dq_i\Big) \, e^{{im\over 2\hbar \, dt}(q_0^2+q_f^2)+\big(\bm{q}^T\cdot\bm{M}\cdot\bm{q} +\bm{v}^T\cdot\bm{q}\big)}\nonumber\\ &=&\int \Big(\sqrt{{im\over 2\pi \hbar \, dt}}\Big)^{N+1} \Big(\prod_{i=1}^{N}dy_i\Big) \, e^{{im\over 2\hbar \, dt}(q_0^2+q_f^2)+\big(\bm{y}^T\cdot\bm{\Lambda}\cdot\bm{y} +(\bm{v}\cdot \bm{O}^T)\cdot\bm{y}\big)}\nonumber\end{eqnarray*}

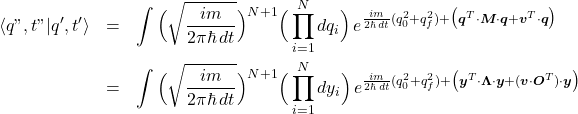
and now we can do the integrals using the Gaussian integration formulas.
Instead of position states, we may want \langle\psi'(t)|\psi(0)\rangle or \langle n'(\infty)|n(-\infty)\rangle where \{|n\rangle\} is some enumerated complete basis, such as Hamiltonian eigenstates. Since any state can be expanded in such a complete basis, including position states

    \[|q(t)\rangle=e^{i\hat{H}t}|q\rangle=\sum_n e^{i\hat{H}t}|n\rangle \langle n|q\rangle=\sum_n \psi^*_n(q)\, e^{iE_nt}|n\rangle\]

    \[ \langle n|q(t)\rangle=\psi^*_n(q)\, e^{iE_nt} \]

Consider then

(5)   \begin{eqnarray*} \langle n(T)|n'(t)\rangle&=& \int dq_1\cdots dq_{N}\langle n(T)|q_{N}\rangle\langle q_N|q_{N-1}\rangle\langle q_{N-1}|q_{N-2}\rangle\cdots \langle q_2|q_{1}\rangle\langle q_1|n'(t)\rangle\nonumber\\ &=& \int dq_1\cdots dq_{N}\langle n(T)|q_{N}\rangle\, T\prod_j e^{{i\over \hbar}L(q_j,\dot{q}_j) dt} \, \langle q_1|n'(t)\rangle\nonumber\\ &=&\int dq_1\cdots dq_{N}\, \psi^*_n(q_{N})e^{-iE_nT} \, T\prod_j e^{{i\over \hbar}L(q_j,\dot{q}_j) dt}\, \psi_{n'}(q_{1})e^{iE_{n'}t} \nonumber\\ & &\mbox{replace $H\rightarrow (1-i\epsilon)H$, resulting $L$ is $L'$}\nonumber\\ &=&\int dq_1\cdots dq_{N}\, \psi^*_n(q_{N})e^{-i(1-i\epsilon)E_nT} \, T\prod_j e^{{i\over \hbar}L'(q_j,\dot{q}_j) dt}\, \psi_{n'}(q_{1})e^{i(1-i\epsilon)E_{n'}t} \nonumber\\ \langle n(\infty)|n'(-\infty)\rangle&=&\left\{\begin{array}{ll} 0 & n\ne 0, \quad n'\ne 0\\ \int dq_1\cdots dq_{N}\, \psi^*_0(q_{N}) \, e^{{i\over \hbar}\int_{-\infty}^\infty L'(q,\dot{q}) dt}\, \psi_{0}(q_{1}) & n=n'=0\end{array}\right. \nonumber\end{eqnarray*}

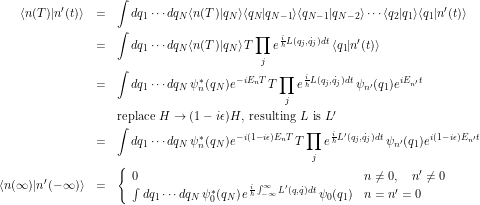
absorbing the values of the wavefunctions at the now quite arbitrary endpoint of the path integration,

    \[ \langle 0(\infty)|0(-\infty)\rangle=\int \mathcal{D}[q] \, e^{{i\over \hbar}\int_{-\infty}^\infty L' dt}=\int \mathcal{D}[q] \mathcal{D}[p] \, e^{{i\over \hbar}\int_{-\infty}^\infty (p\dot{q}-(1-i\epsilon)H) dt}\]

The oscillator
You can do exactly the same procedure for the oscillator using the results from 711

    \[S={1\over 2}m\omega^2(q^2+\alpha^2)\cot\omega t-{\alpha m\omega\over \sin\omega t} \, q\]

Here is the calculation: start with

    \[ L={1\over 2} m \dot{x}^2 -{1\over 2} m\omega^2 x^2\]

we can compute the path integral by subdividing the time T into N parts such that

(6)   \begin{eqnarray*}S(x_0,0; x_f, T)&=& \sum_{i=1}^N dt {1\over 2} m\Big( {(x_1-x_0)^2\over dt^2}+{(x_2-x_1)^2\over dt^2}+\cdots +{(x_f-x_N)^2\over dt^2}\nonumber\\ &-&\omega^2{(x_1+x_0)^2\over 2^2}-\omega^2{(x_2+x_1)^2\over 2^2}-\cdots-\omega^2 {(x_f+x_N)^2\over 2^2}\Big)\nonumber\end{eqnarray*}

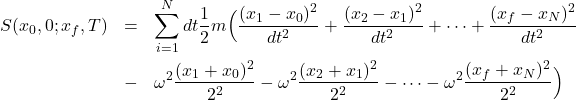
in which we computed the potential at the midpoint of each interval in order to get a symmetrical matrix representation. The exponent of the path integral will then be

    \[ {im\over 2\hbar dt}(1-{\omega^2 dt^2\over 4})(x_0^2+x_f^2)+ \mathbf{x}^T\cdot\stackrel{\leftrightarrow}{M}\cdot\mathbf{x}+\mathbf{v}^T\cdot\mathbf{x}\]

in which the matrix \stackrel{\leftrightarrow}{M} is tridiagonal, just like it was for the free particle, with diagonal entries

    \[\lambda= {im\over \hbar \, dt}-{im\omega^2 dt\over 4\hbar}={im\over \hbar \, dt}(1-{\omega^2 dt^2\over 4})\]

and the off-diagonal entries are

    \[x=-{im\over 2\hbar \, dt}-{im\omega^2 dt\over 8\hbar}=-{im\over 2\hbar \, dt}(1+{\omega^2 dt^2\over 4})\]

and once again the vector \mathbf{v} is null with only first and last components being nonzero

    \[ \mathbf{v}_i=-({im\over \hbar \, dt}+{im\omega^2 dt\over 4\hbar}) \, (x_0\delta_{i,1}+x_f\delta_{i,N})\]

Everything that we did to evaluate the free-particle path integral remains valid except for the precise form of the determinant and inverse matrix elements. We find in this case that

    \[ \Lambda={im\over 2\hbar \, dt}(1-{\omega^2 dt^2\over 4}\pm \sqrt{1-2{\omega^2 dt^2\over 4}-(1+2{\omega^2 dt^2\over 4})}\approx {im\over 2\hbar \, dt}(1\pm {i\omega dt}-{\omega^2 dt^2\over 4})\approx {im\over 2\hbar \, dt} \, e^{\pm i\omega \, dt}\]

and so

    \[ \tilde{D}_N=({im\over 2\hbar \, dt})^N {\sin(N+1) \omega \, dt\over \sin \omega \, dt}\approx ({im\over 2\hbar \, dt})^N {\sin(N+1) \omega \, dt\over \omega \, dt}\approx ({im\over 2\hbar \, dt})^N {\sin\omega T \over \omega \, dt}\]

and

    \[ (M^{-1})_{1,1}={\tilde{D}_{N-1}\over \tilde{D}_N}={2\hbar \, dt\over im} {\sin(N) \omega \, dt\over \sin(N+1)\omega \, dt}\approx {2\hbar \, dt\over im}(1-\omega \, dt \, \cot\omega T)\]

using (N+1) dt=T.
Furthermore

    \[(M^{-1})_{1,N}={(-1)^{N-1} x^{N-1}\over \tilde{D}_N}={({im\over 2\hbar \, dt})^{N-1} (1+{\omega^2 dt^2\over 4})^{N-1}\over ({im\over 2\hbar \, dt})^{N} {\sin \omega T\over \omega dt}}={2\hbar \over im}{\omega \, dt^2 \over \sin \omega T}\]

We can put the parts together and in the final expression involving the exponential of

    \[ -{1\over 4} \mathbf{v}^T\cdot \stackrel{\leftrightarrow}{M}^{-1}\cdot \mathbf{v}\]

we multiply out terms and arrange things in increasing powers of dt;

    \[ -{1\over 4} \mathbf{V}^T\cdot \stackrel{\leftrightarrow}{M}^{-1}\cdot \mathbf{v}= {1\over dt}\big( -{m\over 2\hbar i}(x_0^2+x_f^2)\big)+ \big({m\omega \over 2i\hbar}(x_0^2+x_f^2) \, \cot \omega T -{m\omega \over \hbar i}{x_0 x_f\over \sin\omega T}\big)+\mathcal{O}(dt^1)\]

We arrive at the following result (compare with the 711 action which you got by solving a generating function differential equation in problem set 11!)

    \[ (\sqrt{{i m\over 2\pi \hbar dt}})^{N+1} \sqrt{{\pi^N \over ({im\over 2\hbar dt})^N {\sin\omega T\over \omega \, dt}}} \, e^{{m\over 2\hbar i dt}(x_0^2+x_f^2)-{m\over 2\hbar i dt}(x_0^2+x_f^2)+ \big({m\omega \over 2i\hbar}(x_0^2+x_f^2) \, \cot \omega T -{m\omega \over \hbar i}{x_0 x_f\over \sin\omega T}\big)}\] \[=\sqrt{{m\omega \over 2\pi \hbar \sin\omega T}} \, e^{{m\omega \over 2i\hbar}(x_0^2+x_f^2) \, \cot \omega T -{m\omega \over \hbar i}{x_0 x_f\over \sin\omega T}}=\int\mathcal{D}[x(t)] \, e^{{i\over \hbar}S(x_0,0;x_f,T)}\]

Related Posts

Protected: Physics 711: Lecture 28
Protected: 711: Lecture 5
Protected: Physics 711: PS-6 solutions
Home 2.0
error: Content is protected !!