The divergence of the correlation length 
signals the formation of a special global state, a state of scale invariance. This is very much unlike the global states of thermodynamics which are homogeneous and non-local. The scale-invariant states of the transitioning ferromagnet are very much non-homogeneous with dramatic local fluctuations. It is a “new” kind of global structure, the kind seen in self-similar constructions in fractal geometry and chaotic dynamics.
Right at the critical point, the correlation functions and other “
-point” functions take on a very special form. We saw the derivation of the Orenstein-Zernicke formula
![\[\langle s(r) \, s(0)\rangle\approx {e^{-r/\xi}\over r^{{d-1\over 2}}}, \qquad \xi=(m\sqrt{d})^{-1}\sim t^{-\nu}\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-b302daba328fd828dd99dc6674a40150_l3.png "Rendered by QuickLaTeX.com")
![\[ \nu={1\over 2}\quad\mbox{since}\quad m^2\sim t\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-0c3d989ff5590b819cd16f0e5b833e44_l3.png "Rendered by QuickLaTeX.com")
right at the critical point
![\[\langle s(r) \, s(0)\rangle\approx r^{{1-d\over 2}}\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-67b62946d30120da3034275403c36d51_l3.png "Rendered by QuickLaTeX.com")
which has the property that
![\[\langle s(\lambda r) \, s(0)\rangle=\lambda ^{{1-d\over 2}}\langle s(r) \, s(0)\rangle\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-68cd7009bd28e648f37ccaa2205be390_l3.png "Rendered by QuickLaTeX.com")
which is the classic definition of a scale-invariant function (which implies full conformal invariance of the field 
, which can only happen for massless fields); a function 
is scale invariant if there is some 
(the scaling dimension) such that
![\[f(x)=\lambda^{-\Delta} f(\lambda x)\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-a9958b79e12c9340ef8b699ac00c8eba_l3.png "Rendered by QuickLaTeX.com")
Not every function has this property. Pure monomials 
do, polynomials do not, exponentials do not. The scaling hypothesis is that the (most) divergent or dominant part of a function has this feature near (at) the critical point.
The hyperscaling hypothesis attributes the divergence of various thermodynamic functions at the critical point to the divergence of . This “more fundamental” hypothesis stipulates that
The correlation length has such a form
![\[\xi(t,h)=t^{-\nu} f_\xi\Big({h\over t^\Delta}\Big)\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-b774bb991db013c28cc31de479268330_l3.png "Rendered by QuickLaTeX.com")
Close to critical, is the only important length scale and its divergence is entirely responsible for all other quantities becoming singular, if they do so.
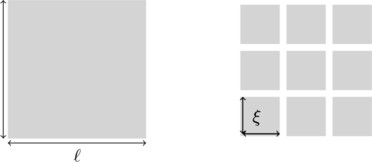
In 
-dimensions, how does the free energy 
or 
scale with the system length 
(it is in a hypercubic box)? It is extensive so, 
and 
. Now divide the system into blocks each of which is the size of the correlation length in every dimension, each contributing a constant factor to the free energy at criticality to construct from 
above a scaling function for the free energy
![\[F(t,h)\sim C \, (\ell/\xi)^d=t^{d\nu} f^{-d}_\xi\Big({h\over t^\Delta}\Big)=t^{d\nu} f_f\Big({h\over t^\Delta}\Big)\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-4fd7b26be8b64c7add12f3944f510f62_l3.png "Rendered by QuickLaTeX.com")
![\[ 2-\alpha=d\nu, \quad \mbox{(Josephson's identity)}\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-261116ecb50389f38084f41054da75cf_l3.png "Rendered by QuickLaTeX.com")
and so the hyperscaling hypothesis has as a consequence the scaling hypothesis. Furthermore we can eliminate 
in favor of and deduce that since
![\[E\sim t^{1-\alpha}, \qquad E\sim t^{1-\alpha}\sim \xi^{-({1-\alpha\over \nu})}\sim {1\over \xi^{{d\nu-1\over \nu}}}={1\over \xi^{d-{1\over \nu}}}\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-fab76d8db81fddfba53a8ba6bae2ea29_l3.png "Rendered by QuickLaTeX.com")
which is a hint that the “fields” become scale-invariant functions of inter-spin distances at the critical point, a prelude to conformal field theory and the conformal bootstrap hypothesis.