Simple model Hamiltonians for quantum particles of all types have free-particle parts such as
![]()
(for bosons we would have)
![]()
which simply counts up the number of excitations in the system and multiplies by the energy of the excitation, and interaction parts that contain more creation/annihilation operators. We will study simple interacting systems by first establishing what their ground states look like, and then studying low-lying excitations by various linearization techniques. We do so systematically, we first study the ground states.
Let’s denote the (fermion) absolute vacuum by ![]() , and a quantum state containing one electron of momentum
, and a quantum state containing one electron of momentum ![]() and spin
and spin ![]() by
by ![]() and a two electron state with momenta/spin
and a two electron state with momenta/spin ![]() and
and ![]() by
by ![]() .
.
Note that a proper fermion state must obey the exclusion principle
![]()
Let’s define a “first in, first out” notation
![]()
The required Pauli exclusion principle is satisfied if the annihilation/creation operators anti-commute
![]()
Note that
![]()
Let a system of ![]() independent non-relativistic (
independent non-relativistic (![]() ) fermions have quantum Hamiltonian
) fermions have quantum Hamiltonian
![]()
The ground state ![]() (illustrated below) is the state with
(illustrated below) is the state with
![]()
![]()

Let’s prove that the modified Hamiltonian
![]()
has zero vacuum expectation value
![]()
For the Fermi gas illustrated,
![]()
and since ![]() ,
, ![]() .
.
Properties of the Fermi-Dirac vacuum/GS
![]() What is the total spin of the Fermi ground state
What is the total spin of the Fermi ground state ![]()
![]()
![]() What is the total momentum of the Fermi ground state
What is the total momentum of the Fermi ground state ![]()
![]()
so the filled Fermi-sea ground state has no net spin or momentum,
![]() and using
and using ![]() to measure its energy it has no net energy.
to measure its energy it has no net energy.
This is a rather good model of a filled energy band in a crystalline solid. It certainly explains the electrical conductivity (none!) of a filled band.
Bogoliubov transformations: a quantum canonical transformation
We invent new operators
![]()
![]()
![]()
for ![]() both above and below the Fermi momentum.
both above and below the Fermi momentum.
To see this, rewrite the operators in terms of an angle variable
![Rendered by QuickLaTeX.com \[\tilde{b}_{\mathbf{k}, s}=\cos\theta_k \, b_{\mathbf{k}, s}+\sin\theta_k \, b^\dagger_{-\mathbf{k}, \bar{s}}, \qquad \theta_k=0, \quad k>k_f, \quad \theta_k=\pi/2, \quad k\le k_f\] \[\tilde{b}^\dagger_{\mathbf{k}, s}=\cos\theta_k \, b^\dagger_{\mathbf{k}, s}+\sin\theta_k \, b_{-\mathbf{k}, \bar{s}}, \qquad \theta_k=0, \quad k>k_f, \quad \theta_k=\pi/2, \quad k\le k_f\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-024afe1ecfa3d482e3fe9dad0176efa2_l3.png)
in which ![]() or
or ![]() , and
, and ![]() when
when ![]() ,
, ![]() when
when ![]() . This gives us the commutation relations we seek, and we can easily compute
. This gives us the commutation relations we seek, and we can easily compute
(1) 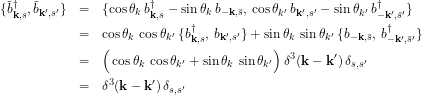
since ![]() and the anticommutator of two
and the anticommutator of two ![]() ‘s or two
‘s or two ![]() ‘s are zero.
‘s are zero.
Describe the states
![]()
for the system represented in the figure above, illustrated in the ![]() state. For example we can see that
state. For example we can see that
![]()
is a state with a filled vacuum but with a vacancy or hole in the ![]() position.
position. ![]() , and this state has spin
, and this state has spin ![]() and momentum
and momentum ![]() .
.
![]()
is a state with a filled vacuum but with a vacancy or hole in the ![]() position.
position. ![]() , and this state has spin
, and this state has spin ![]() and momentum
and momentum ![]() .
.
The ![]() operators create holes in the otherwise filled Fermi sea if
operators create holes in the otherwise filled Fermi sea if ![]() , these holes have positive energy relative to
, these holes have positive energy relative to ![]() .
.
![]()
is a state with a filled vacuum plus an additional quanta above the Fermi level. ![]() , and this state has spin
, and this state has spin ![]() and momentum
and momentum ![]() .
.
Let’s work on writing ![]() in terms of the new annihilation/creation operators, lets start with
in terms of the new annihilation/creation operators, lets start with
(2) 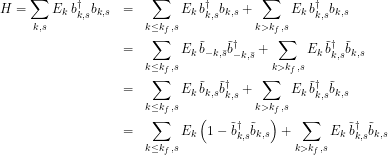
now consider that any particle moved out of the set ![]() must be moved into the set
must be moved into the set ![]() ,
,
(3) 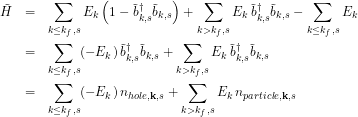
and so the number of holes equals the number of particles excited above the Fermi level, so
![]()
and we can add zero onto ![]() to get
to get
(4) 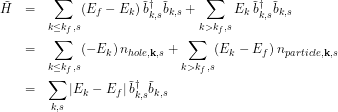
in effect the “zero point” of the energy has been moved to the Fermi sea surface and the Fermi vacuum has zero energy. In statistical physics and condensed matter physics we study phenomena that preserve ![]() , so any process creating a hole in the Fermi sea creates a filled state or quanta above it. In other words
, so any process creating a hole in the Fermi sea creates a filled state or quanta above it. In other words ![]() where the “p,h” refer to particle excitation and hole.
where the “p,h” refer to particle excitation and hole.
This means that in any equilibrium process ![]() , a property that you will many times in particle and condensed matter physics.
, a property that you will many times in particle and condensed matter physics.
If we use only the new annihilation/creation operators and ![]() , the Fermi ground state is effectively a “vacuum”, which has two interesting types of excitations, “particles” and “holes”. Note that creating a hole is an excitation with a positive energy.
, the Fermi ground state is effectively a “vacuum”, which has two interesting types of excitations, “particles” and “holes”. Note that creating a hole is an excitation with a positive energy.