Physics 449: Wells and barriers

Consider now an inverted barrier or well such as that in the figure, $V=-V_0$ for $0\le x\le \ell$ .
The physics of this system is much the same, we have “free streams” in all three regions

$k={\sqrt{2mE}\over \hbar}, \quad \mu=\frac{\sqrt{2m(E+V_0)}}{\hbar}$

(1) $\begin{eqnarray*}\psi_I(x)&=&e^{ikx}+R \, e^{-ikx}\nonumber\\ \psi_{II}(x)&=&B_1 \, e^{i\mu x}+B_2 \, e^{-i\mu x}\nonumber\\ \psi_{III}(x)&=& T \, e^{ikx}\end{eqnarray*}$

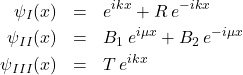
It is a good exercise to show that (hint hint)

(2) $\begin{eqnarray*} B_1={2({\mu\over k}+1)\over (1+{\mu\over k})^2-(1-{\mu\over k})^2 e^{2i\mu \ell}}, &\qquad& B_2={2({\mu\over k}-1)e^{2i\mu \ell}\over (1+{\mu\over k})^2-(1-{\mu\over k})^2 e^{2i\mu \ell}}\nonumber\\ R={(1-{\mu^2\over k^2})(1-e^{2i\mu \ell})\over (1+{\mu\over k})^2-(1-{\mu\over k})^2 e^{2i\mu \ell}}, &\qquad& T={4{\mu\over k}e^{i\mu \ell-ik\ell}\over (1+{\mu\over k})^2-(1-{\mu\over k})^2 e^{2i\mu \ell}}\end{eqnarray*}$

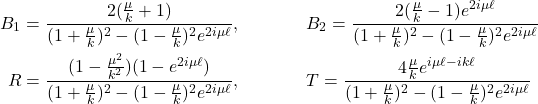
Careful investigation shows that there are special wavenumbers $k$ for which the potential well is transparent or reflectionless to the incoming monochromatic wave.

As it turns out we can use what we learned about the simple step “up” with $V=0$ to the left of $x=0$ , $V=V_0$ to the right of $x=0$ with $\psi_L=e^{ikx}+R_1e^{-ikx}$ , $\psi_R=T_1 e^{i\mu x}$ to solve this problem rather intuitively, drawing from the methods of Physics 207 and 325 where multiple internal reflections were studied. I posted the relevant material from those courses a few days back, so please have a look.

The idea is simple: we build the overall reflection coefficient $R$ by considering multiple internal reflections at $x=0,x=\ell$ .
$\bullet$ Step 1. A wave $1\cdot e^{ikx}$ arrives at $x=0$ with phase $1$ . A fraction of it $R_1={k-\mu\over k+\mu}$ reflects (primary reflection), a fraction $C_1={2k\over k+\mu}$ penetrates $x=0$ and passes into region II.
$\bullet$ This wave of amplitude $C$ flows to $x=\ell$ by which distance it has accumulated phase $e^{i\mu\ell}$ . A fraction of this total wave $T_2Ce^{i\mu \ell}$ penetrates into region III, a fraction $DCe^{i\mu \ell}$ reflects from $x=\ell$ and heads back towards $x=0$ .
$\bullet$ . This wave flows to $x=0$ and in the process accumulates additional phase $e^{i\mu\ell}$ , so the total wave has amplitude/phase $DCe^{2i\mu \ell}$ by time it reaches $x=0$ . This wave splits at $x=0$ , fraction $T_1DCe^{2i\mu \ell}$ penetrates $x=0$ into region I (the secondary wave) and combines with the primary wave.
A fraction $BDCe^{2i\mu \ell}$ where $B={2\mu\over k+\mu}$ reflects back into region II and flows towards $x=\ell$ .
$\bullet$ This wave reaches $x=\ell$ accumulating additional phase $e^{i\mu\ell}$ in the process. The arriving wave $BDCe^{3i\mu \ell}$ splits, a fraction $T_2BDCe^{3i\mu \ell}$ penetrates $x=\ell$ and flows into region III, a fraction $DBDCe^{3i\mu \ell}$ reflects and flows back towards $x=0$ .
$\bullet$ The left moving wave $DBDCe^{3i\mu \ell}$ at $x=\ell$ arrives back at $x=0$ as $DBDCe^{4i\mu \ell}$ . A fraction $T_1DBDCe^{4i\mu \ell}$ passes through $x=0$ into region I and combines with primary and secondary reflections. A fraction $BDBDCe^{4i\mu \ell}$ reflects back into II and flows towards $x=\ell$ .
$\bullet$ Repeat this an infinite number of times. In the figure below I have “exploded” the view, points $a,c,e,g$ are all the same point $x=\ell$ , points $b,d,f,\cdots$ are all the same $x=\ell$

We now use formulas such as

$1+a+a^2+a^3+\cdots={1\over 1-a}, \quad |a|<1$

to add up all of the reflected wave amplitudes to get the total reflected amplitude:

$R=R_1+T_1CDe^{2i\mu\ell}\Big(1+(BDe^{2i\mu\ell})+(BDe^{2i\mu\ell})^2+\cdots\Big)$

$=R_1+{T_1CD\over 1-BD e^{2i\mu\ell}}$

$={k-\mu\over k+\mu}+{{2\mu\over k+\mu}{2k\over k+\mu}(\tfrac{\mu-k}{ \mu+k})e^{2i\mu\ell}\over 1+(\tfrac{\mu-k}{ \mu+k})(\tfrac{k-\mu}{ \mu+k})e^{2i\mu\ell}}$

$={k-\mu\over k+\mu}\Big({(\mu+k)^2-(\mu-k)^2e^{2i\mu\ell}-4\mu k e^{2i\mu\ell}\over (\mu+k)^2-(\mu-k)^2e^{2i\mu \ell}}\Big)$

$R=\Big({(k-\mu)(k+\mu)(1-e^{2i\mu\ell})\over (\mu+k)^2-(\mu-k)^2e^{2i\mu \ell}}\Big)$

You can play the same game to sum up all waves transmitted into region III to get $T$ .
Bound states
These have energy $E={\hbar^2 k^2\over 2m}$ for imaginary $k$ values corresponding to poles of $T$ , ie those $k$ for which

$(\mu+k)^2-(\mu-k)^2e^{2i\mu \ell}}=0, \quad \pm\Big({\mu+k\over \mu-k}\Big)=e^{i\mu\ell}$

The first can be simplified to

$- i{\mu\over k}=\cot(\mu\ell/2)$

OK now watch the birdie..

$-i\sqrt{{E\over E+V_0}}=\cot(\sqrt{{2m(E+V_0)\over \hbar^2}}{\ell\over 2}), \quad -\sqrt{{-E\over E+V_0}}=\cot(\sqrt{{2m(E+V_0)\over \hbar^2}}{\ell\over 2})$

but these energies are negative: $E=-|E|$ for them

$-\sqrt{{|E|\over V_0-|E|}}=\cot(\sqrt{{2m(V_0-|E|)\over \hbar^2}}{\ell\over 2})$

If the well is really deep ie $V_0\rightarrow \infty$ then we expect that $E=-V_0+KE$ and for low-lying levels KE will be small

$-\sqrt{{V_0-KE\over KE}}\approx -\infty =\cot(\sqrt{{2m(KE)\over \hbar^2}}{\ell\over 2})$

and an inspection of cotangent show that it is negative infinite near $n\pi$ :

$E\approx -V_0+{\hbar^2 (2n\pi)^2\over 2m\ell^2}$

which is what we expect, a PIB-type limiting case. For the second case ( $- i{k\over \mu}=\cot(\mu\ell/2)$ ) we get the rest (replace $2n$ with $2n-1$ ).

Tunneling
The tunneling of a particle right through a potential barrier, to emerge on the other side, is a purely quantum mechanical effect with no classical analog. It is the basis for almost all of solid state electronics and is responsible for the behavior of p-n junctions and transistors, so it is no exaggeration to say that it is one of the most important physical phenomena to have an understanding of. Contemplate a barrier of potential $V_0$ and width $a$ in an otherwise zero potential region of the $x-$ axis, and let particle of energy $E<V_0$ be incident on it from the left. There will be reflected waves, and waves transmitted into the barrier and even beyond. Within the barrier there will be both left and right moving waves because of reflection from both junctions, $x=0$ , and $x=a$ , although they must have complex momentum to be in a classically forbidden region.
We will get the solution from our previous example with a few judicial replacements, starting with $\ell\rightarrow a$ .

From the figure we can divide space into three regions and propose the wavefunction in each region to be (for $E<V_0$ )

(3) $\begin{eqnarray*}\psi_I&=&e^{ikx}+Re^{-ikx}, \nonumber\\ \psi_{II}&=&B_1 e^{Kx} +B_2 e^{-Kx}\nonumber\\ \psi_{III}&=&T e^{ikx} \end{eqnarray*}$

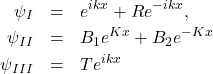
where the momenta are

$k=\frac{\sqrt{2mE}}{\hbar}, \qquad K=\frac{\sqrt{2m(V_0-E)}}{\hbar}$

Let’s write the solution down from our square well by noting that the replacement $\mu\rightarrow -iK$ transforms the wavefunctions in the well $0\le x\le \ell$ into those in the barrier $0\le x\le a$ . We then get $T$ for free by making these replacements in the well solution

$T=\frac{-4ik}{K}\frac{e^{-ika}}{e^{Ka}(1-\frac{ik}{K})^2 -e^{-Ka}(1+\frac{ik}{K})^2}$

The modulus of this amplitude is called the tunneling amplitude

$|T|^2=\frac{4k^2}{K^2}\frac{1}{\frac{4k^2}{K^2} \cosh^2(Ka) +(1-\frac{k^2}{K^2})^2 \sinh^2{Ka}}$

$=\frac{1}{1+\frac{1}{4}(\frac{k}{K}+\frac{K}{k})^2 \sinh^2(Ka)} \rightarrow e^{-2Ka}$

The last limit is valid for $Ka>>1$ , and is actually a very good approximation for the probability of tunneling through the barrier per encounter.
Example
A particle stream of energy $E$ and flux density $\mathcal{F}=10^8 /s\cdot cm^2$ (number of particles per second per beam cross-sectional area) encounters a barrier of height $V_0=2E$ and thickness $a=\lambda$ where $\lambda$ is the particle de’Broglie wavelength. How many particles per second per cross-sectional area penetrate the barrier?