Quantum computation is the use of a quantum system to act as a computing device. The optional problem set two problem in which you showed that a quantum system can act as a perfect random number generator was a nice example:
Apply a Hadamard gate to a ground state ![]()
and then apply a measurement operator, ![]() which produces
which produces ![]() randomly with equal probability, but do it for a
randomly with equal probability, but do it for a ![]() -bit system
-bit system
![]()
Here’s a nice number operator
![]()
For a 4 bit system find the eigenvalues of ![]() , and use Bell.jl to make 30,000 measurements of
, and use Bell.jl to make 30,000 measurements of ![]() on
on ![]() . Make a histogram of the results, and explain how this system of 4 qubits can be used as a 4 bit true random number generator.
. Make a histogram of the results, and explain how this system of 4 qubits can be used as a 4 bit true random number generator.
In existing computer systems random numbers are generated by algorithms that do not produce true random numbers. For example we can create a list of pseudo random numbers with a congruential generator ![]()
with ![]() and
and ![]() (
(![]() is the Lehmer RNG). Such numbers are not truly random, but the outcomes of measurements on quantum systems are genuinely random.
is the Lehmer RNG). Such numbers are not truly random, but the outcomes of measurements on quantum systems are genuinely random.
The problem solution is as follows:
include("Bell.jl")
using .Bell
ψ=(HG*ψ₀)⊗(HG*ψ₀)⊗(HG*ψ₀)⊗(HG*ψ₀)
H1=ψ₀⊗ψ₀'
Nb=H1⊗u⊗u⊗u+2*u⊗H1⊗u⊗u+4*u⊗u⊗H1⊗u+8*u⊗u⊗u⊗H1
mymeasurements=[measurement(ψ,Nb)[1] for j in 1:30000
using FreqTable
mytable=freqtable(mymeasurements)
bar([j for j in 0:15],mytable ./30000)
savefig("QCprob-1.png")
Those possible 4-bit numbers ![]() are measurement outcomes of equal likelihood, but of course we are using a classical computer to simulate the behavior of a quantum measurement process.
are measurement outcomes of equal likelihood, but of course we are using a classical computer to simulate the behavior of a quantum measurement process.
Encoding information as bits
Classical bits are ![]() ,
, ![]() , a quantum bit is a superposition
, a quantum bit is a superposition
![]()
only measurable things are ![]() and
and ![]() since
since ![]() and
and ![]() represent the same quantum state.
represent the same quantum state.
A quantum system with ![]() qubits contains the information of
qubits contains the information of ![]() complex numbers, so modeling such a system with a classical computer will require storage of a vast amount of floating point data.
complex numbers, so modeling such a system with a classical computer will require storage of a vast amount of floating point data.
We typically create the qubits (superpositions) by applying gates such as a Hadamard gate, to a state that could be interpreted as a classical bit such as ![]() . So we will want to transform data such as ords or numbers into bitstrings such as
. So we will want to transform data such as ords or numbers into bitstrings such as ![]() and in a quantum system with
and in a quantum system with ![]() qubits we would want to use this object as an input. creating a state
qubits we would want to use this object as an input. creating a state ![]() that computational gates can be applied to.
that computational gates can be applied to.
So the first order of business is transforming words or numbers into bitstrings. This is done by coding.
Coding is about sending a discrete variable ![]() observed at point “A” to point “B” by a network using codes of
observed at point “A” to point “B” by a network using codes of ![]() signals. Let the message be composed of discrete values
signals. Let the message be composed of discrete values ![]() for example. These may represent letters like
for example. These may represent letters like ![]() ,
, ![]() and so forth, in some language. They are encoded by assigning them unambiguously to sequences of
and so forth, in some language. They are encoded by assigning them unambiguously to sequences of ![]() in a reversible way
in a reversible way
![]()
(all require two bits) or
![]()
(ine 1-bit, two 2-bit, one 3-bit) are both allowed, since no sequence can be made by taking a shorter one and adding more terms, that would lead to ambiguities.
![]()
For economy it is best to use codings that require a minimal number of bits: that depends of the character frequency of the language, In English, not all letters are used with the same frequency to compose words (see https://www3.nd.edu/~busiforc/handouts/cryptography/letterfrequencies.html), for example in a random word the probability that a given letter is an E is 0.111 but the probability that it is a Q is 0.0019. Suppose that in our four-letter language
![]()
then any message using the first coding requires
![]()
bits per character on average, and the second coding
![]()
bits/character sent, and so is preferable.
For messages comprised of symbols ![]() encoded as bit-strings of lengths
encoded as bit-strings of lengths ![]() , valid encodings must obey
, valid encodings must obey
![]()
{\bf Proof}. Let ![]() equal the number of
equal the number of ![]() ‘s that are equal to
‘s that are equal to ![]() (for the first case above
(for the first case above ![]() ,
, ![]() ,
, ![]() , and for the second case
, and for the second case ![]() ,
, ![]() ,
, ![]() ,
, ![]() ).
).
![Rendered by QuickLaTeX.com \[\begin{array}{ll}w_1\le 2 & \mbox{since we only have bits $0,1$}\\ w_2\le 2^2-2w_1 & \mbox{can't tack a $0,1$ onto a length-$1$ code}\\ w_3\le 2^3-2^2w_1-2w_2& \mbox{can't tack $00,01,10,11$ onto a length-$1$}\\ & \mbox{or a $0,1$ onto a length-$2$ code}\\ \end{array}\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-c9c9c8599fdc1c0195745a087bb0ea32_l3.png)
so in general
![]()
since the ![]() counts the number of
counts the number of ![]() ‘s equal to
‘s equal to ![]() .
.
Noiseless coding theorem
![]()
The right hand side is the Boltzmann entropy (equal to the information entropy or statistical surprise) of statistical physics.
Proof: Use the theorem with ![]()
![]()
(1) 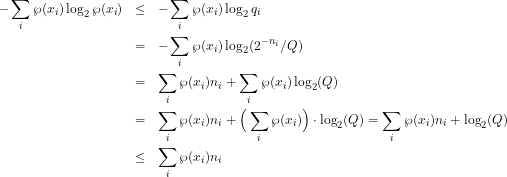
since
![]()
The right side is the length of a typical coded single character. The theorem defines a place for the entropy or surprise function ![]() of probability theory and statistical physics in coding theory.
of probability theory and statistical physics in coding theory.
Source coding is a mapping from a sequence of symbols from an information source to a sequence of alphabet symbols (usually bits) such that the source symbols can be exactly recovered from the binary bits (lossless source coding) or recovered within some distortion (lossy source coding). This is the concept behind data compression.
Shannon’s coding theorem
![]() independent and identically distributed random variables
independent and identically distributed random variables ![]() each with entropy
each with entropy
![]()
can be compressed into more than ![]() bits with negligible risk of information loss, as
bits with negligible risk of information loss, as ![]() , but if they are compressed into fewer than
, but if they are compressed into fewer than ![]() bits it is virtually certain that information will be lost.
bits it is virtually certain that information will be lost.
Quantum information
Consider ![]() and
and ![]() . Apply
. Apply ![]() to each, and in the first case we get
to each, and in the first case we get ![]() , in the second we get
, in the second we get ![]() half of the time. The
half of the time. The ![]() measurement result reveals nothing about which state was measured, there is no way to reliably distinguish between these two states by this measurement.
measurement result reveals nothing about which state was measured, there is no way to reliably distinguish between these two states by this measurement.
In quantum error correction the data of a qubit is stored in a highly entangled multi-qubit state, protecting it against loss by noise or bad gates. Thermal interactions between the qubit quantum systems and the environment can cause a qubit to flip or change states, cosmic ray collisions can do the same, and a quantum computer will be highly susceptible to errors created by such processes. How can errors and data loss be detected and corrected in a system of qubits? Suppose that thermal interactions have a probability ![]() of flipping a qubit. We will soon study how
of flipping a qubit. We will soon study how ![]() depends on temperature
depends on temperature ![]() .
.
Bit flip gates;
![]()
![]() Encode the states
Encode the states ![]() as
as ![]() and
and ![]() as
as ![]()
![]() Encode the qubit
Encode the qubit ![]() as
as ![]()
![]() Pass each qubit through an independent copy of the bit flip gate. The probability that all qubits were flipped is
Pass each qubit through an independent copy of the bit flip gate. The probability that all qubits were flipped is ![]() , that two or more qubits were flipped is
, that two or more qubits were flipped is ![]() .
.
In what follows we will assume that at most one qubit is flipped and not describe detection/correction of multiple flips.
Construct the following four mutually compatible projection operators
![]()
and
![]()
![]()
which detect flipped bits on first, second or third qubits. The operators project onto the bit-flipped state vectors. Let
![]()
be an “error syndrome” operator, whose eigenstates are the original and single qubit-flipped stste-vectors. Note that if there are no qubits flipped
![]()
and if the first qubit is flipped
![]()
so that depending on the measurement outcome for the error syndrome, we recover the state and can apply a suitable gate to reconstruct from it the original data (do nothing if the error syndrome is ![]() , apply a bit-flipping gate to qubit two if the error syndrome is
, apply a bit-flipping gate to qubit two if the error syndrome is ![]() , and so forth).
, and so forth).