Suppose you have a code that needs to perform a very large number of similar integrations over the same interval, for example you need to compute several thousand Hamiltonian matrix elements for hydrogenic states for an interaction Hamiltonian that will be modified at each loop cycle. You can choose from Trapezoid, Romberg, Clenshaw, or Gaussian quadrature and embed the integration routine in your code rather than make a function call to an external library. Better still you can memoize your internal function calls so that a given integration is never performed from scratch twice.
Gaussian quadrature makes the fewest computations.
A Gaussian quadrature or integration formula is an expression of the form
![Rendered by QuickLaTeX.com \[\int_{-1}^1 w(x) \, f(x) \, dx=\sum_{n=0}^N \lambda_k \, f(x_k)\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-830f86263bc3ad84eee2b75c5aa8de33_l3.png)
in which the ![]() are suitably chosen points. Such a formula can be very much faster to evaluate than Simpson’s rule or the Trapezoid rule, and can give comparable or even improved accuracy. The formula is constructed using a set of orthogonal polynomials
are suitably chosen points. Such a formula can be very much faster to evaluate than Simpson’s rule or the Trapezoid rule, and can give comparable or even improved accuracy. The formula is constructed using a set of orthogonal polynomials ![]() such that
such that
![]()
and by requiring that the formula be exact for all polynomial arguments ![]() of degree less than or equal to
of degree less than or equal to ![]() . since there are
. since there are ![]() weights
weights ![]() and
and ![]() valuation points
valuation points ![]() . The extreme case is such that
. The extreme case is such that ![]() is of degree
is of degree ![]() , in which case it can be written as
, in which case it can be written as
![]()
Then since ![]() we can write
we can write
![Rendered by QuickLaTeX.com \[\int_{-1}^1 w(x) \, f(x) \, dx= \int_{-1}^1 w(x) \, \Big(\sum_{k=0}^N a_k \phi_k(x) \phi_{N+1}(x) +r_N(x)\Big) \, dx\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-7da9095ec77d4356cec7edbe56b23218_l3.png)
![]()
due to the orthogonality of the polynomials. We have then
![Rendered by QuickLaTeX.com \[\int_{-1}^1 w(x) \, f(x) \, dx=\sum_{k=0}^N \lambda_k \, \Big(q_N(x_k) \, \phi_{N+1}(x_k) +r_N(x_k)\Big)\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-fbe5a84fc00acc5bc98a93b0322738a4_l3.png)
![Rendered by QuickLaTeX.com \[=\sum_{k=0}^N \lambda_k r_N(x_k)\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-fa97302251e093663d03a67e60dece14_l3.png)
implying that the valuation points are roots of ![]()
![]()
To determine the weights we then let
![]()
and discover that this results in ![]() equations for only
equations for only ![]() unknowns
unknowns
![Rendered by QuickLaTeX.com \[\int_{-1}^1 w(x) \, \phi_r(x) \, \phi_s(x) \, dx=\delta_{r,s}= \sum_{k=0}^N \lambda_k \phi_r(x_k) \, \phi_s(x_k)\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-0a99ae477fe01212bfd66331d5422cc4_l3.png)
This is badly over constrained; if we can find any solution that is nontrivial, it is the only solution. We notice that we can write the expression as a matrix equation, using the fact that the unit matrix is the discrete delta function
![Rendered by QuickLaTeX.com \[\left(\begin{array}{ccccc}1&0&0&0&\cdots \\ 0&1&0&0&\cdots \\ 0&0&1&0&\cdots \\ 0&0&0&1&\cdots\\ \cdots&\cdots&\cdots&\cdots&\cdots \end{array}\right) =\left(\begin{array}{ccccc} \sqrt{\lambda_0} \phi_0(x_0)&\sqrt{\lambda_1} \phi_0(x_1)&\sqrt{\lambda_2} \phi_0(x_2)&\sqrt{\lambda_3} \phi_0(x_3)&\cdots\\ \sqrt{\lambda_0} \phi_1(x_0)&\sqrt{\lambda_1} \phi_1(x_1)&\sqrt{\lambda_2} \phi_1(x_2)&\sqrt{\lambda_3} \phi_1(x_3)&\cdots\\ \sqrt{\lambda_0} \phi_2(x_0)&\sqrt{\lambda_1} \phi_2(x_1)&\sqrt{\lambda_2} \phi_2(x_2)&\sqrt{\lambda_3} \phi_2(x_3)&\cdots\\ \sqrt{\lambda_0} \phi_3(x_0)&\sqrt{\lambda_1} \phi_3(x_1)&\sqrt{\lambda_2} \phi_3(x_2)&\sqrt{\lambda_3} \phi_3(x_3)&\cdots\\ \cdots&\cdots&\cdots&\cdots&\cdots \end{array}\right)\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-43344ad14ecc9161c77f828ab29cdd07_l3.png)
![Rendered by QuickLaTeX.com \[\cdot\left(\begin{array}{ccccc} \sqrt{\lambda_0} \phi_0(x_0)&\sqrt{\lambda_0} \phi_1(x_0)&\sqrt{\lambda_0} \phi_2(x_0)&\sqrt{\lambda_0} \phi_3(x_0)&\cdots\\ \sqrt{\lambda_1} \phi_0(x_1)&\sqrt{\lambda_1} \phi_1(x_1)&\sqrt{\lambda_1} \phi_2(x_1)&\sqrt{\lambda_1} \phi_3(x_1)&\cdots\\ \sqrt{\lambda_2} \phi_0(x_2)&\sqrt{\lambda_2} \phi_1(x_2)&\sqrt{\lambda_2} \phi_2(x_2)&\sqrt{\lambda_2} \phi_3(x_2)&\cdots\\ \sqrt{\lambda_3} \phi_0(x_3)&\sqrt{\lambda_3} \phi_1(x_3)&\sqrt{\lambda_3} \phi_2(x_3)&\sqrt{\lambda_3} \phi_3(x_3)&\cdots\\ \cdots&\cdots&\cdots&\cdots&\cdots \end{array}\right)\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-97e687b8b0b251d5f4810aab734a230d_l3.png)
which can be solved uniquely if the array on the right is orthogonal. Then every row and every column is a unit vector. The row condition is one of our constraints, the column conditions are then
![Rendered by QuickLaTeX.com \[1=\lambda_k \sum_{n=0}^N \phi_n^2(x_k)\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-4e6de1b32f355a28b8e0222b81fe88c2_l3.png)
which gives us our sought after weights
![]()
General orthogonal polynomials have a three-point recursion relation
![]()
write this for a nearby ![]() , subtract, and sum
, subtract, and sum
(1) 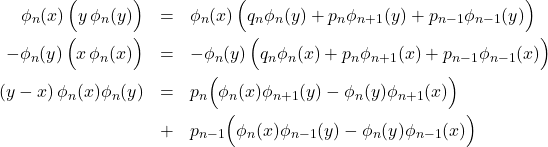
now sum up to ![]() and notice that the last pair of terms cancel one another pairwise, except at the end
and notice that the last pair of terms cancel one another pairwise, except at the end
![Rendered by QuickLaTeX.com \[(y-x) \sum_{n=0}^N \phi_n(x)\phi_n(y)=p_N\Big(\phi_N(x) \phi_{N+1}(y)-\phi_N(y)\phi_{N+1}(x)\Big)\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-45d87386654e624d08657a460f737b8e_l3.png)
Now let ![]() ;
;
![Rendered by QuickLaTeX.com \[\sum_{n=0}^N \phi_n(x)\phi_n(x)=p_N \phi_N(x) {d \phi_{N+1}\over dx} (x)\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-dc03bba09d5e76dae45816f575135544_l3.png)
and we obtain another very useful expression for our weights, since this one does not involve a sum
![]()
Chebyshev polynomials are particularly useful for evaluating integrals with ![]() since with only elementary trigonometric identities one can show that
since with only elementary trigonometric identities one can show that
![]()
which is very significant, all weights are the same. Then the complete integration formula reads
![Rendered by QuickLaTeX.com \[\int_{-1}^1 {f(x)\over \sqrt{1-x^2}} \, dx\approx {\pi\over N+1} \sum_{k=0}^N f\Big( \cos({(2k+1) \pi\over 2(N+1)})\Big)\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-d889f7b7d1d4cffd47784772ddc16b6a_l3.png)
Just how useful is this? Suppose that you must evaluate thousands of integrals of the form ![]() for different
for different ![]() integrands. By the trapezoid rule, you may need hundreds or thousands of subdivisions to get acceptable accuracy, so you may be looking at very long run times.
integrands. By the trapezoid rule, you may need hundreds or thousands of subdivisions to get acceptable accuracy, so you may be looking at very long run times.
For orthogonal polynomials of the form
![Rendered by QuickLaTeX.com \[\phi_n(x)=\sum_{k=0}^n A_{n,k}x^k\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-965347148fead89dd5a32edc6951876e_l3.png)
it is easy to show that
![]()
the ratio of the coefficients of the highest powers of ![]() in the polynomials. For Chebyshev polynomials the recursion relation and
in the polynomials. For Chebyshev polynomials the recursion relation and ![]() indicates that
indicates that
![]()
Using the orthonormal set
![]()
we find that
![]()
after some simple arithmetic, as indicated above.
The domain ![]()
One very useful application of Gaussian quadrature is the construction of a method for computing integrals of functions over an infinite domain. Clearly the trapezoid rule or Simpson’s rule cannot be used in such cases. Suppose that we have an integral
![]()
For example if we choose ![]() and
and ![]() ,
, ![]() , then we should perform a Gaussian quadrature using functions orthogonal with respect to measure
, then we should perform a Gaussian quadrature using functions orthogonal with respect to measure ![]() on the interval, namely
on the interval, namely
![]()
the Hermite polynomials, and the ![]() are the roots
are the roots ![]() for some very high
for some very high ![]() . Our quadrature formulas developed above tell us that
. Our quadrature formulas developed above tell us that
![]()
It is a good exercise to prove that
![]()
from the formula for the weights, and the properties of the Hermite functions. All you need to do in order to accurately evaluate integrals over the infinite domain is to select a sufficiently large ![]() , and accurate determine the roots of
, and accurate determine the roots of ![]() .
.
Here is a loadable lisp package that gives you all five integration schemes, it is easy to rewrite in the language of your choice,
(defpackage :quadrature
(:use :common-lisp)
(:nicknames "quadr")
(:documentation "Basic numerical integration functions (JRS 2015)")
(:export :Trapezoid
:Romberg
:Clenshaw
:Gaussian
:LagGauss))
; ;; to use, make it the current package
(in-package :quadrature)
(defun Trapezoid (fcn n a b)
"Trapezoid rule integration n divisions, from a to b (make sure a, b are doubles);
(TrapezoidQuad (fcn n a b))"
(let* ((h (/ (- b a) n))
(s (/ (+ (funcall fcn a) (funcall fcn b)) 2.0d0)))
(* h (+ s (loop for j from 1 to (- n 1) sum (funcall fcn (+ a (* h j))))))))
(defun Romberg (fcn n a b)
"Romberg integration using the trapezoid function with 2^n divisions
(make sure a, b are doubles); (Romberg (fcn n a b))"
(let* ((M (make-array '(20 20))) (x (/ 1.0d0 4.0)))
(loop for i from 1 to N do (setf (aref M i 1)
(Trapezoid fcn (expt 2 (- i 1)) a b)))
(loop for i from 2 to N do
(loop for j from 2 to i do
(setf (aref M i j)
(/ (- (aref M i (- j 1)) (* (expt x (- j 1))
(aref M (- i 1) (- j 1)))) (- 1 (expt x (- j 1)))))))
(format t "~S~%" (aref M N N))))
(defun Clenshaw (fcn n L)
"Clenshaw-Curtis integration for [-OO <= x <= OO], pick L (a double),
(ClenshawQuad (fcn n L))"
(flet ((sq (x) (* x x)))
(let* ((prefactor (/ (* L pi) n))
(weights (loop for j from 1 to (- n 1) collect
(/ 1.0d0 (sq (sin (/ (* j pi) n))))))
(abscissa (loop for j from 1 to (- n 1) collect
(funcall fcn (/ L (tan (/ (* j pi) n)))))))
(* prefactor (apply #'+ (mapcar #'(lambda (x y) (* x y)) weights abscissa))))))
(defun Gaussian (fcn N)
"Gaussian quadrature of fcn for [-1<= x <= 1], N-point, (GaussianQuad (fcn N))"
(setq foo (loop for k from 0 to N collect
(funcall fcn (cos (/ (* (+ (* 2.0d0 k) 1.0d0) pi ) (+ 2.0d0 (* 2.0d0 N)))))))
(/ (* pi (apply #'+ foo)) (+ N 1.0d0)))
(defun LagGauss (fcn)
"30 pt Gauss-Laguerre quadrature from [0 <= x<= infty] of a function,
(LagGaussQuad (fcn))"
(let* ((x
'(0.047407180540804851462d0 0.24992391675316022399d0 0.61483345439276828461d0
0.11431958256661007983d1 0.18364545546225722914d1 0.26965218745572151957d1
0.37258145077795089493d1 0.49272937658498824096d1 0.63045155909650745228d1
0.78616932933702604687d1 0.96037759854792620798d1 0.11536546597956139701d2
0.13666744693064236295d2 0.16002221188981066255d2 0.18552134840143150124d2
0.21327204321783128928d2 0.24340035764532693401d2 0.27605554796780961028d2
0.31141586701111235818d2 0.34969652008249069544d2 0.39116084949067889122d2
0.43613652908484827807d2 0.48503986163804200427d2 0.53841385406507505617d2
0.59699121859235495477d2 0.66180617794438489652d2 0.81736810506727685722d2
0.91556466522536838255d2 0.10126170079110515587d3))
(w '(0.11604408602039325562d0 0.22085112475069602168d0 0.24139982758787346417d0
0.19463676844641672701d0 0.12372841596688099224d0 0.63678780368988269342d-1
0.26860475273380519412d-1 0.93380708816042351497d-2 0.26806968913369005386d-2
0.63512912194087764641d-3 0.12390745990688661704d-3 0.19828788438952961056d-4
0.25893509291314845838d-5 0.2740942840536085164d-6 0.23328311650257961683d-7
0.15807455747783781037d-8 0.84274791230570478547d-10 0.34851612349079771461d-11
0.1099018059753472728d-12 0.25883126649592354135d-14 0.44378380598403008663d-16
0.53659183082123539538d-18 0.43939468922917157784d-20 0.2311409794388649359d-22
0.72745884982925408326d-25 0.12391497014482743994d-27 0.98323750831056357112d-31
0.28423235534027969144d-34 0.18786080317495715679d-38 0.15715421886653993432d-42)))
(setf fs (loop for y in x collect (funcall fcn y)))
(reduce #'+ (mapcar #'* w fs))))
;;; to list the exported symbols in a package...
;;; (do-external-symbols (s (find-package "quadrature")) (print s))
;;; function documentation
;;; (documentation 'LagGaussQuad 'function)
(defun f (x)
(* x (- 1.0d0 x) (log (* x (- 1 x)))))
Download from http://abadonna.physics.wisc.edu/download/numerical-integration/