Let be a symmetric matrix (this is rather important). Perform a decomposition , and create a new matrix

note that the order of the factors is reversed. It was noted that the off-diagonal matrix elements shrink in the process, but of course the eigenvalues and determinant are unchanged, since

and we know that orthogonal transformations do not alter the eigenvalues, and a matrix can be diagonalized by repeated orthogonal transformation.
Now decompose into and construct

Then

This process can be continued, and under the right set of conditions (if was a symmetric matrix), one eventually reaches a transformed that is approaching a diagonalized or triangularized state, as the off-diagonal (above, below the main diagonal or both) elements shrink to below machine precision. This is one of the most powerful and general diagonalization algorithms ever discovered.

The QR algorithm for eigenvalue extraction for a symmetric matrix is a repeated decomposition followed by a matrix multiplication

Perform the decomposition of
create
Perform the decomposition of
create
Continue this process: and stop the process when the matrix elements of below the main diagonal are smaller than , or after iterations.

# in julia, using CUDA to load onto the gpu
# use the QR decomposition in the LinearAlgebra library
using LinearAlgebra
using CUDA
# try it on a 256x256 array
b=rand(256,256);
b=b+b';
B=CuArray(b);
for j in 1:600
QR=qr(B)
B=QR.R * CuArray(QR.Q)
end
collect(B[j,j] for j in 1:256)
# Full eigenvalue extraction to 64 bits in 28 seconds on jetson nano

The only way to speed this up is to do it on the gpu, or to diminish the size of the matrix as you procede (deflation), or to improve convergence by shifting. Let be the unit matrix

Create an empty list of eigenvalues.
Let be the lower right corner diagonal entry of and be the unit matrix. Perform the decomposition of
Make
Let be the lower right corner diagonal entry of . Perform the decomposition of
Make
Continue this process until you get to some level such that all matrix elements in the last row of except for the one on the diagonal, the rightmost element, are smaller than . Then add this last row rightmost element of to the list of eigenvalues.
Form by removing the last row and column from , and repeat the whole
process on the smaller array.
Do this until the array is deflated to a , then add its only element to the eigenvalue list.

# Implementation in R using Rmpfr multiple precision arrays
eigenval <- function(M,precision,iters){
  N <- ncol(M)
  cp <- Rmpfr::mpfrArray(rep(0,N^2),prec=64, dim = c(N, N))
  cp <- M
  eigs <- c()
  for (j in 1:iters){
    if (N==1){eigs <- c(eigs,cp)
              break}
    c<- cp[N,N]
    for (k in 1:N){cp[k,k]<- cp[k,k]-c}
    qr <- QR(cp)
    cp <- qrq
    for (k in 1:N){cp[k,k]<- cp[k,k]+c}
    if (max(abs(cp[N,-N]))<=precision) {
       eigs <- c(eigs,cp[N,N])
       cpn <- Rmpfr::mpfrArray(rep(0,(N-1)^2),prec=64, dim = c(N-1, N-1))
       cpn<- cp[1:(N-1),1:(N-1)]
       cp<- cpn
       N<-N-1 }
    }
    return(eigs)
    }

Convert this to julia and run it on the gpu, and we diagonalize the in seconds.

Any matrix can be factored

into the product of an orthogonal matrix and an upper-triangular matrix , and Gram-Schmidt points the way. Think of it like this: the rows or columns of a non-singular matrix (one whose determinant is not zero) are a set of linearly independent vectors. These vectors can be transformed into a set of orthogonal unit vectors via GS.

Let’s do it then: start out with two linearly independent vectors and and create a matrix . Lets pick and normalize it, and use the result as

Note that

(1)  

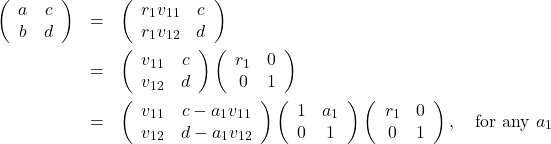
so we pick . Note that the second column of the new matrix is to the first column, so it must be , where

(2)  

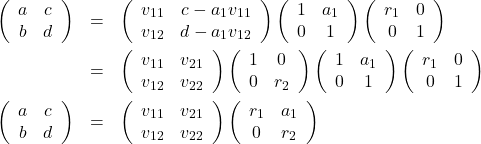
We began with an arbitrary matrix and decomposed it into a product of an orthogonal matrix (made of orthogonal unit vectors ) and an upper-triangular matrix .

Let’s do it for three linearly independent vectors , ,and , and make a matrix out of them

Stage 0. Let , then

Stage 1. Let , then

let , and ;

Final stage, let , and

Call , and ;

if you multiply it all out

a full decomposition of our original arbitrary matrix.