The LU decomposition is a factoring of an arbitrary square matrix into an upper-triangular and lower-triangular pair of factors. This factoring is very useful for solving linear equations, since the inversion of such upper/lower matrices is trivial. We select a standard form for the lower triangular matrix; ones on its diagonal. For example
![Rendered by QuickLaTeX.com \[\left(\begin{array}{ccc}2&-1&-2\\ -4&6&3\\ -4&-2&8\end{array}\right)=\left(\begin{array}{ccc}1&0&0\\ -2&1&0\\ -2&-1&1\end{array}\right)\left(\begin{array}{ccc}2&-1&-2\\ 0&4&-1\\ 0&0&3\end{array}\right)\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-05e3731e4eceed7b1a0ba1796eeb8a72_l3.png)
LU decomposition can be done very efficiently, it is significantly faster and easier to program than QR decomposition, and it is technically much simpler.
![]() Start with
Start with
![Rendered by QuickLaTeX.com \[LU=\left(\begin{array}{ccc}1&0&0\\ L_{21}&1&0\\ L_{31}&L_{32}&1\end{array}\right)\left(\begin{array}{ccc}U_{11}&U_{12}&U_{13}\\ 0&U_{22}&U_{23}\\ 0&0&U_{33}\end{array}\right)\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-080f15136f35626c97aed8ed65591ebd_l3.png)
![Rendered by QuickLaTeX.com \[=\left(\begin{array}{ccc}m_{11}&m_{12}&m_{13}\\ m_{21}&m_{22}&m_{23}\\ m_{31}&m_{32}&m_{33}\end{array}\right)=M\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-fb7a32eb41c02cc1dd91cf31660a2039_l3.png)
Dotting the first row of ![]() into each column of
into each column of ![]() we see
we see
![]()
![]() Now dot the second row of
Now dot the second row of ![]() into each column of
into each column of ![]() and solve
and solve
![]()
Solve the first equation, so ![]() is known, now solve the remaining equations for
is known, now solve the remaining equations for ![]() :
:
![]()
so the second rows of both ![]() and
and ![]() are gotten from
are gotten from ![]() and the first row of
and the first row of ![]()
You can see that if ![]() , the process fails at the very first stage, and so we usually perform a permutation or pivot
, the process fails at the very first stage, and so we usually perform a permutation or pivot ![]() that rearranges the rows of of
that rearranges the rows of of ![]() so that
so that ![]() has the property that
has the property that ![]() for all
for all ![]() . In other words the diagonal entries of
. In other words the diagonal entries of ![]() are larger in absolute value than any entries below them in the same column. We apply the LU algorithm to the permuted matrix
are larger in absolute value than any entries below them in the same column. We apply the LU algorithm to the permuted matrix
![]()
# in R
Pivot <- function(M){
N <- ncol(M)
P <- matrix(rep(0,N^2),nrow=N,ncol=N)
for (k in 1:N){P[k,k]<- 1.0}
Mc <- M
for (k in 1:(N-1)){
largest <- which.max(abs(Mc[k:N,k]))
if(largest>1){
Mc[c(k,largest+k-1),] <- Mc[c(largest+k-1,k),]
P[c(k,largest+k-1),] <- P[c(largest+k-1,k),]}
}
return (list("perm"=P,"matrix"=Mc))
}![]() Finally dot the last row of
Finally dot the last row of ![]() into
into ![]() ;
;
![]()
Solve the first, now ![]() is known, use this to solve the second
is known, use this to solve the second
![]()
so now ![]() known, and the third equation contains one unknown
known, and the third equation contains one unknown
![]()
Some computations (for example the first row of ![]() ) can be saved by copying
) can be saved by copying ![]() into
into ![]() immediately and creating the rest of
immediately and creating the rest of ![]() right on top of
right on top of ![]() , destroying
, destroying ![]() in the process (construction in situ)
in the process (construction in situ)
# this R code returns L,U,P
U <- function(M){
N <- ncol(M)
L <- matrix(rep(0,N^2),nrow=N,ncol=N)
U <- matrix(rep(0,N^2),nrow=N,ncol=N)
Q <- Pivot(M)
for (i in 1:N){
for (k in i:N){
sm <- -sum(L[i,1:i]*U[1:i,k])
U[i,k] <- Q$matrix[i,k]+sm}
for (k in i:N){
if(i==k){L[i,i] <- 1.0}
else{sm <- -sum(L[k,1:i]*U[1:i,i])
L[k,i]<- (Q$matrix[k,i]+sm)/U[i,i]}
}
}
return (list("l"=L,"u"=U,"p"=t(Q$perm)))
}Inverting triangular linear systems
Back substitution
![Rendered by QuickLaTeX.com \[\left(\begin{array}{cccc} u_{11}& u_{12} & \cdots & u_{1n}\\ 0 & u_{22} & \cdots & u_{2n}\\ \vdots & \vdots & \ddots &\vdots\\ 0 & \cdots & 0 & u_{nn}\end{array}\right)\left(\begin{array}{c} x_1\\ x_2\\ \vdots\\ x_n\end{array}\right)= \left(\begin{array}{c} b_1\\ b_2\\ \vdots\\ b_n\end{array}\right)\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-785acc1fb463d9f80dc948cb77ca1a9f_l3.png)
(1) 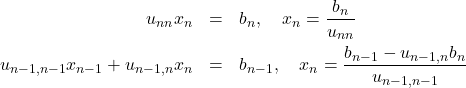
so for the ![]() row element
row element
![]()
Forward substitution
![Rendered by QuickLaTeX.com \[\left(\begin{array}{cccc} \ell_{11}&02} & \cdots & 0\\ \ell_{21} & \ell_{22} & \cdots & 0\\ \vdots & \vdots & \ddots &\vdots\\ \ell_{n1} & \ell_{n2} & \cdots & \ell_{nn}\end{array}\right)\left(\begin{array}{c} x_1\\ x_2\\ \vdots\\ x_n\end{array}\right)= \left(\begin{array}{c} b_1\\ b_2\\ \vdots\\ b_n\end{array}\right)\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-b976d980ce24d3f4e51f09370fca02ba_l3.png)
(2) 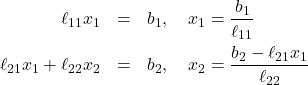
![]()
Fsub <- function(L,b){
N <- ncol(L)
y <- matrix(rep(0,N),nrow=N,ncol=1)
for (j in 1:N){
y[j]<- (b[j]-sum(L[j,1:(j-1)]*y[1:j-1]))/L[j,j]}
return(y)
}
To write a solver for ![]() ,
,
![]() apply the LU decomposition
apply the LU decomposition
![]()
![]() solve
solve ![]() for
for ![]() , then
, then
![]() solve
solve ![]() for
for ![]() .
.
You probably can’t write any linear algebra code that can compete with GEMM or the solvers in LAPACK and BLAS when it comes to speed, but the point of “rolling your own” is to learn the algorithms, and to create self-contained codes that don’t require numerous calls to external libraries.