A Pade’ approximant is a rational approximation to a function ![]() of the form
of the form
={\sum_{j=0}^M p_jx^j\over 1+\sum_{j=1}^L q_jx^j}\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-132d885179c0a0290d09d1659becfb7a_l3.png)
It can be computed very algorithmically from a Taylor series
expansion of the function
![]()
First cut the Taylor series off at ![]() and multiply it out,
and multiply it out,
![Rendered by QuickLaTeX.com \[\sum_{j=0}^M p_jx^j-\Big(\sum_{n=0}^{L+M} a_n x^n\Big)\Big(1+\sum_{j=1}^L q_jx^j}\Big)=0\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-28547c869d73f5caa679d72f8534681d_l3.png)
Equate like coefficients on each side, a process that results in two
sets of equations
(1) 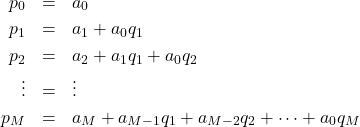
(2) 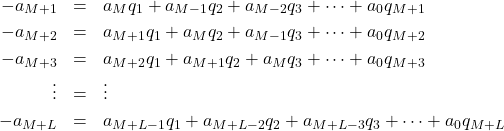
however ![]() for
for ![]() on the right-hand side.
on the right-hand side.
Solve the second set for ![]() and use it in the first
and use it in the first
set to get the ![]() .
.
We can do this in REDUCE
operator p,q,a,eqtn,rhs;
q(0):=1;
!M:=3;
!L:=5;
matrix !T(!L,!L);
matrix inhom(!L,1);
Numerator:=for j:=0:!M sum p(j)*x^j$
Denominator:=for j:=0:!L sum q(j)*x^j$
Func:=for j:=0:(!M+!L) sum a(j)*x^j$
zilch:=Denominator*Func-Numerator$
for j:=0:(!M+!L) do eqtn(j):=coeffn(zilch,x,j);
for j:=1:!L do for k:=1:!L do !T(k,j):=df(eqtn(k+!M),q(j));
for j:=1:!L do inhom(j,1):=eqtn(j+!M)-for k:=1:!L sum !T(j,k)*q(k);
soln:=-1/!T*inhom$
for j:=1:!L do let q(j)=soln(j,1)$
for j:=0:!M do let solve(eqtn(j),p(j))$
a(0):=1; a(1):=1; a(2):=1/2; a(3):=1/6; a(4):=1/24; a(5):=1/120; a(6):=1/720;a(7):=1/5040;a(8):=1/40320;
pade:=numerator/denominator;
As you can see I set this up so that we will get the ![]() approximant to
approximant to ![]() . Let’s run it:
. Let’s run it:
pade:=numerator/denominator;
3 2
- x - 12*x - 60*x - 120
pade := ----------------------------
3 2
x - 12*x + 60*x - 120In a previous post on recursions, we worked out the Miller algorithm for computing Bessel functions using a descending three-term recursion. This type of algorithm, in which the final step is a”renormalization” using an addition identity, leads to a Pade’ approximant. For example we start with ![]() and
and ![]() , the descending recursion
, the descending recursion ![]() terminating in
terminating in ![]() together with
together with ![]() leads to
leads to
4 2
3*x - 128*x + 640
J_0(x) := ---------------------
4 2
x + 32*x + 640
So what is the application to critical phenomena? Suppose that a function ![]() has singular behaviour at some critical value
has singular behaviour at some critical value ![]() , in which
, in which ![]() is regular. Then its logarithmic derivative has a pole there
is regular. Then its logarithmic derivative has a pole there
![]()
so that the residue of the logarithmic derivative at ![]() is
is ![]()
![]()
One of the most influential models of strong interactions in two dimensions is to consider a triangular lattice of ![]() lattice points on which non-overlapping hexagons will be placed. The activity of a single hexagon is
lattice points on which non-overlapping hexagons will be placed. The activity of a single hexagon is ![]() , and the system has a critical point at a density below the close-packing density of
, and the system has a critical point at a density below the close-packing density of ![]() .
.
A series expansion for ![]() can be approximated by a Pade’ approximant
can be approximated by a Pade’ approximant ![]()
![]()
![Rendered by QuickLaTeX.com \[={b_0+b_1z+\cdots +b_M z^M\over 1+c_1z+\cdots+c_Nz^N}={P_M(z)\over c_N\prod_{j}^N(z-z_j)}\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-9e92a86c548d648bb666240c1ec12c3c_l3.png)
which is a ratio of an ![]() order polynomial and an
order polynomial and an ![]() order polynomial, in which the zeroes of
order polynomial, in which the zeroes of ![]() are the poles/singularities of
are the poles/singularities of ![]() . All computer algebra systems have a Pade’ approximant function and a real root finding function.
. All computer algebra systems have a Pade’ approximant function and a real root finding function.
A triangular lattice of ![]() can be divided into three sublattices “1”, “2”, “3”. Consider a completely filled up or covered lattice in which every site of type “1” has a hexagon on it (we could start with all “2” sites or all “3” sites covered). Now we can create a “hole” or anti-hexagon with activity
can be divided into three sublattices “1”, “2”, “3”. Consider a completely filled up or covered lattice in which every site of type “1” has a hexagon on it (we could start with all “2” sites or all “3” sites covered). Now we can create a “hole” or anti-hexagon with activity ![]() by removing a hexagon from a site. Doing so we find high-density formulas for the densities each of the three sublattices
by removing a hexagon from a site. Doing so we find high-density formulas for the densities each of the three sublattices
![]()
![]()
The total density is ![]() .
.
An order parameter for the phase transition (solid-fluid) is
![]()
Use your favorite computer CAS to find Pade’ approximants ![]() and
and ![]() for
for ![]() in variable
in variable ![]() . One root of
. One root of ![]() will persist to a root of
will persist to a root of ![]() , use it to find the critical activity
, use it to find the critical activity ![]() . The order parameter critical exponent is
. The order parameter critical exponent is ![]() ,
, ![]() with
with ![]() , find
, find ![]() . Let’s use REDUCE, and load its own pade library (not use our DIY above)…
. Let’s use REDUCE, and load its own pade library (not use our DIY above)…
!R:=1-z-6*z^2-43*z^3-347*z^4-3002*z^5;
load(pade);
load(roots);
dlogR:=taylortostandard(taylor(df(log(!R),z),z,0,7));
!Q:=pade(dlogR,z,0,3,3);
realroots(den(!Q));
# {z= - 0.0119137,z=0.0142508,z=0.0877545} last is persistent
!Q:=pade(dlogR,z,0,2,2);
realroots(den(!Q));
# {z=0.0899435,z=0.300713} see?
# so z_c=11.11809, very close to the exact value, the model is exactly solvable
sub(z=0.0899435, num(!Q)/(z-0.300713));
# 0.108764605959 Exact value is 1/9=beta, you are very close