Algorithms: Finite Element Methods-I. Galerkin method

Finite element methods (FEM) are used to solve a vast array of problems in all disciplines, it is essential to learn these methods if you really want to use the computer to solve real-world problems. I will illustrate some of the commonly used methods, but this is a large discipline of itself, so you will want to get a good book on the subject and read it through.
A one-dimensional differential equation
Lets solve the problem of simple cooling of a body

${df(t)\over dt}=-\lambda f, \qquad f(0)=f_0$

$\bullet$ Break up the domain into a mesh of points. These do not need to be equally spaced. For example let the entire time domain be $0\le t\le 1$ (so a series solution could be convergent), and so that everything can be numerical let $\lambda=2.0$ and $T_0=10$ . We will break up the interior domain into $t_1=0.2$ , $t_2=0.5$ , $t_3=0.85$ .
$\bullet$ Construct a trial solution that obeys the boundary condition using some basis functions , here we use powers of $t$

$f_{trial}=f_0+f_1 t+f_2 t^2+f_3 t^3+\cdots$

which we truncate so that we have as many undetermined constants as we do interior mesh points

$f_{trial}=10.0+f_1 t+f_2 t^2+f_3 t^3$

$\bullet$ Construct the residual function which measures how close the trial is to the actual solution;

$R={df_{trial}\over dt}+\lambda f_{trial}=10.0\lambda+(1+\lambda t) \, f_1+(2t+\lambda t^2) \, f_2+(3t^2+\lambda t^3) \, f_3$

$=20.0+(1+2t) \, f_1+(2t+2 t^2) \, f_2+(3t^2+2 t^3) \, f_3$

$\bullet$ Find the coefficients $f_i$ that minimize the residual. Note the similarity to least squares.
It may be possible to actually force the residual to vanish (collocation method). This will happen when we have a set of linear equations in the coefficients to solve.
For a collocation solution, we obtain a system of equations using our mesh of $t$ -values:

(1) $\begin{eqnarray*} R(t_1)&=&0.136 \, f_3 + 0.48 \, f_2 + 1.4 \, f_1 + 20\nonumber\\ R(t_2)&=& f_3 + 1.5 \, f_2 + 2 \, f_1 + 20\nonumber\\ R(t_3)&=&3.39775 \, f_3 + 3.145 \, f_2 + 2.7 \, f_1 + 20\end{eqnarray*}$

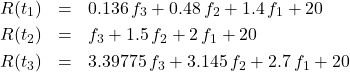
Solving these we obtain

$f_1=-19.1315, \qquad f_2=15.5811, \qquad f_3=-5.108$

which is not in good agreement with the exact solution $f=10 \, e^{-2t}=10-20 \, t+20 \, t^2-13.33 \, t^3+\cdots$ .
Let’s write a REDUCE program (REDUCE is great for prototyping because it is not strongly typed) and try to get better accuracy

operator a,eqs;
trial:=10.0+for n:=1:8 sum a(n)*x^n;
mesh:={0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.85};
R:=df(trial, x)+2.0*trial;
for n:=1:8 do eqs(n):=sub(x=part(mesh,n),R);
solve(for n:=1:8 collect eqs(n), for n:=1:8 collect a(n));

now we get

$f=10-19.99997 t+19.9996769 t^2-13.33096 \, t^3+6.65632681t^4-2.638248t^5+\cdots$

which is much better (obviously a finer mesh will give better results).

Approximating the solution with a polynomial using powers of $t$ or $x$ as a basis creates a problem; fitting a function to a polynomial at a set of discrete points results in oscillation of the polynomial between the discrete set of points used to fit the curve. FEM techniques are designed to cure this problem.

Galerkin method
Instead of demanding the vanishing of the residual, which may not even be possible,we demand that its weighted average value computed over sub-domains vanishes;

$\int_{t_i}^{t_j} W(t) \, R(t) \, dt=0$

and the weight function used in the Galerkin method is the trial function itself. This gives the method a very quantum mechanical flavor, since we will want our basis functions that we expand the trial solution in to be square-integrable, and independent.

The full Galerkin treatment for a one-dimensional problem then is as follows:
Find a set of basis functions $\{\phi_n \, | \, n=1, \cdots, N\}$ and a function $\phi_0$ that obeys the boundary conditions, and construct the trial solution

$f_{trial}(x)=\phi_0+\sum_{n=1}^N f_n \, \phi_n(x)$

(lets assume we are working with functions of $x$ for $0\le x\le 1$ ). Compute the residual $R(t)$ , and then obtain your system of equations

$0=\int_0^1 \phi_n(t) \, R(t) \, dt, \qquad n=1,2,\cdots, N$

and solve the system for your solution.

The most commonly used basis functions for simple demonstrations of the Galerkin method are piecewise continuous localized simplexes in one dimension, with compact support (the subset of $[0, \, 1]$ upon which the function is non-zero)

$\phi_i(x)=\left\{\begin{array}{ll} 1-{|x-i\cdot a|\over a} & (i-1)a\le x\le (i+1)a\\ 0 & \mbox{otherwise}\end{array}\right.$

for the simple reason that

$\phi_i(x)\phi_j(x)=0, \qquad |i-j|>1$

and

${d\phi_i\over dx}=\left\{\begin{array}{ll} {1\over a} & (i-1)a\le x\le ia\\ -{1\over a} & ia\le x\le (i+1)a\\ 0 & \mbox{otherwise}\end{array}\right.$

although localized, compactly supported quadratic and cubic functions are also used. Note that these basis functions are very good for enforcing Neumann boundary conditions ${df\over dx}\Big{|}_{0,1}=c$ since they have constant slopes, and the “overlap integrals” are easy to compute

$\int_0^1 \Big({d\phi_i(x)\over dx}\Big) \, \Big({d\phi_j(x)\over dx}\Big) \, dx=\left\{\begin{array}{ll} {2\over a} & i=j\\ -{1\over a} & |i-j|=1\\ 0 &\mbox{otherwise}\end{array}\right.$

Next: We solve the one-dimensional Dirichlet problem by the Galerkin method.

Home 2.0

Algorithms: Finite Element Methods-I. Galerkin method

Related Posts

Algorithms: Finite Element Methods-I. Galerkin method

Published by Jeff on September 25, 2021September 25, 2021

Related Posts

Eigenvalue extraction with QR decomposition

ML/AI: Feature selection in decision trees (information entropy)

Auto-differentiation: make a julia package