Physics 7xx: Baker-Campbell-Hausdorff relation in QM

Published by Jeff on November 18, 2021November 18, 2021
Jeff

Physics 7xx: Baker-Campbell-Hausdorff relation in QM

Time ordering
We begin with the Schrodinger equation

    \[ \hat{H}(t) \psi(t)=i\hbar{\partial\over \partial t}\psi(t)\]

which we rewrite as

    \[H(t) \psi(t) \, dt=i\hbar\Big(\psi(t+dt)-\psi(t)\Big), \quad \mbox{or}\quad \psi(t+dt)=(1-{i\over \hbar} \hat{H}(t) \, dt) \psi(t)\]

which we iterate starting at t=0 or some other initial time

(1)   \begin{eqnarray*}\psi(dt)&=&\Big(1-{i\over \hbar} \hat{H}(0) \, dt\Big) \psi(0)\nonumber\\ \psi(2 \, dt)&=&\Big(1-{i\over \hbar} \hat{H}(1\, dt) \, dt\Big) \, \psi(dt)=\Big(1-{i\over \hbar} \hat{H}(1 \, dt) \, dt\Big)\Big(1-{i\over \hbar} \hat{H}(0 \, dt) \, dt\Big) \, \psi(0)\nonumber\\ \psi(3 \, dt)&=&\Big(1-{i\over \hbar} \hat{H}(2\, dt) \, dt\Big) \psi(2 \, dt)=\Big(1-{i\over \hbar} \hat{H}(2\, dt) \, dt\Big)\Big(1-{i\over \hbar} \hat{H}(1 \, dt) \, dt\Big)\Big(1-{i\over \hbar} \hat{H}(0 \, dt) \, dt\Big)\psi(0)\nonumber\\ \vdots &=& \vdots\nonumber\\ \psi(n \, dt)&=&\Big(1-{i\over \hbar} \hat{H}((n-1) \, dt) \, dt\Big)\Big(1-{i\over \hbar} \hat{H}((n-2) \, dt) \, dt\Big)\cdots \Big(1-{i\over \hbar} \hat{H}(0) \, dt\Big) \, \psi(0)\end{eqnarray*}

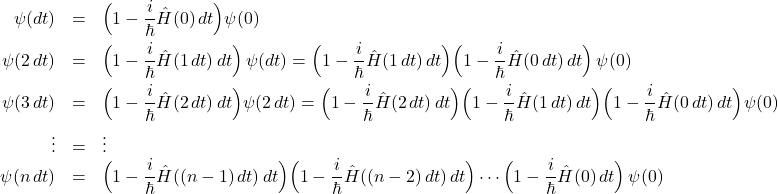
and finally express this as exponentials by neglecting terms of order dt^2, using

    \[\Big(1-{i\over \hbar} \hat{H}(m \, dt) \, dt\Big)\approx e^{-{i\over \hbar} \hat{H}(m \, dt) \, dt}+\mathcal{O}(dt^2)\]

    \[\psi(n \, dt)=e^{-{i\over \hbar} \hat{H}((n-1) \, dt) \, dt} \, e^{-{i\over \hbar} \hat{H}((n-2) \, dt) \, dt} \cdots e^{-{i\over \hbar} \hat{H}(1\, dt) \, dt} \, e^{-{i\over \hbar} \hat{H}(0) \, dt} \, \psi(0)\]

Note that the individual factors are time-ordered, “early” operators act first, in order of the times m \, dt forming their arguments.
We now define time ordered or path ordered exponentiation

    \[\psi(t) = \mathcal{T} \, e^{-{i\over \hbar} \int_0^t \hat{H}(t') \, dt'} \, \psi(0)\]

in which the time ordering unrolls the exponential into a product of operators, with the “earliest” farthest to the right, acting first on the wavefunction. Time ordering in the time evolution operator because [\hat{H}(t),\hat{H}(t')]\ne 0 is why we will need the BCH relation.

Heisenberg and Schrodinger pictures
In the Schrodinger picture the operators are time independent and states, described by wavefunctions \psi(x,t) or kets |\psi(t)\rangle are time dependent,their time evolution is determined by the Schrodinger equation. This can be compactly stated with

    \[|\psi(t)\rangle =U(t,t_0)|\psi(t_0)\rangle \]

Let \hat{A}A be an operator and compute it’s expectation value

    \[\langle \psi(t)|\hat{A}|\psi(t)\rangle =\langle \psi(t_0)|\hat{U}^{\dagger}(t,t_0)|\hat{A}|\hat{U}(t,t_0)|\psi(t_0)\rangle \]

and now define the Heisenberg picture of the state \psi

    \[|\psi_H\rangle =\hat{U}^{\dagger}(t,t_0)|\psi(t)\rangle =\hat{U}^{\dagger}(t,t_0)|\psi_S (t)\rangle \]

and the Heisenberg picture of the operator \hat{A}

    \[\hat{A}_H=\hat{U}^{\dagger}(t,t_0)\, \hat{A}_S \, \hat{U}(t,t_0) \]

in which \hat{A}_S=\hat{A} the time independent representation (Schrodinger picture) of the operator. The expectation value is unaffected by this transformation

    \[\langle \psi_H|\hat{A}_H(t)|\psi_H\rangle =\langle \psi_S(t_0)|\hat{U}^{\dagger}(t,t_0)\, \hat{A}_S \, \hat{U}(t,t_0)|\psi_S(t_0)\rangle =\langle \psi_S(t)|\hat{A}_S|\psi_S(t)\rangle \]

The analytical form of the Heisenberg picture of \hat{A} can be easily found from a differential equation,but you must take care to properly order the operators because in general they do not commute.
Recall that

    \[i\hbar \dot{\hat{U}}=\hat{H}\hat{U}, \qquad -i \hbar \dot{\hat{U}}^{\dagger}=\hat{U}^{\dagger}\hat{H} \]

and \hat{H} is Hermitian so that \hat{H}=\hat{H}^{\dagger}. then

(2)   \begin{eqnarray*}\frac{d}{dt}\hat{A}_H&=&\frac{d}{dt}(\hat{U}^{\dagger}\hat{A}_S \hat{U})=\dot{\hat{U}}^{\dagger} \, \hat{A}_S \, \hat{U}+\hat{U}^{\dagger}\dot{\hat{A}}_S \, \hat{U}+ \hat{U}^{\dagger} \, \hat{A}_S\, \dot{\hat{U}} \nonumber\\ &=&\frac{i}{\hbar}(\hat{U}^{\dagger} \, \hat{H} \, \hat{A}_S \, \hat{U} -\hat{U}^{\dagger} \, \hat{A}_S \, \hat{H} \, \hat{U})+\hat{U}^{\dagger} \dot{\hat{A}}_S \, \hat{U} \nonumber\\ i\hbar \frac{d}{dt} \hat{A}_H&=&\hat{U}^{\dagger} \, [\hat{A}_S,\hat{H}] \, \hat{U}+i\hbar \hat{U}^{\dagger}\dot{\hat{A}}_S \, \hat{U}\nonumber\\ &=&[\hat{A}_H,\hat{H}]+i\hbar\Big(\frac{d}{dt}A_S\Big)_H \nonumber\end{eqnarray*}

If \hat{A}_S is time independent (no explicit t in its expression) like x or -i\hbar\frac{d}{dx} then the last term is zero and we find

    \[i\hbar\frac{d}{dt}\hat{A}_H=[\hat{A}_H,\hat{H}] \]

For example consider the oscillator operators \hat{a} and \hat{a}^{\dagger}. The commutators can be found in any representation and converted since \hat{U}\hat{H}=\hat{H}\hat{U}

(3)   \begin{eqnarray*}i\hbar\frac{d}{dt} \hat{a}_H(t)&=&\hat{U}^{\dagger} \, [\hat{a},\hbar\omega\Big(\hat{a}^{\dagger} \hat{a}+\frac{1}{2}\Big)] \, \hat{U}=\hbar \omega \, \hat{U}^{\dagger}\hat{a}\, \hat{U}=\hbar \omega \, \hat{a}_H \nonumber\\ i\hbar \frac{d}{dt} \hat{a}^{\dagger}_H (t)&=&[\hat{a}^{\dagger}_H, \hat{H}]=-\hbar \omega \hat{a}^{\dagger}_H \nonumber\end{eqnarray*}

which can be integrated to give

    \[\hat{a}_H (t)=e^{-i\omega \, t} \, \hat{a}, \qquad \hat{a}^{\dagger}_H (t)= e^{i \omega \, t} \, \hat{a}^{\dagger}\]

which plays a rather significant role in the construction of the field operators in quantum field theory.

Electromagnetic-stimulated oscillator transitions
Suppose that the Hamiltonian can be split into two parts, one of which contains the interactions of the system with external fields

    \[ \hat{H}=\hat{H}+0+\hat{H}_{int}\]

then the transformation

    \[ \psi_I(t)=e^{{i\over \hbar}\hat{H}_{0} t} \, \psi_S(t), \quad \hat{A}_I(t)=e^{{i\over \hbar}\hat{H}_{0} t} \, \hat{A}_S \, e^{-{i\over \hbar}\hat{H}_{0} t} \]

for which

    \[ i\hbar {d\over dt} \hat{A}_I=[\hat{A}_I, \hat{H}_{int,I}]=e^{{i\over \hbar}\hat{H}_{0} t} \, [\hat{A}_S, \, \hat{H}_{int}] \, e^{-{i\over \hbar}\hat{H}_{0} t} \]

is called the interaction picture, and is used extensively in the quantum field theory of interacting systems.

As an example of an application of a partial Heisenberg picture or interaction picture consider an oscillator that is being stimulated with a time dependent electric field whose potential is

    \[ V(x)=-x \, f(t) \]

the Hamiltonian in the Schrodinger picture is then

    \[\hat{H}=\hbar \omega(\hat{a}^{\dagger} \hat{a} +\frac{1}{2})-f(t)\sqrt{\frac{\hbar}{2m\omega}}(\hat{a}^{\dagger}+\hat{a})=\hat{H}_0 +\hat{H}_{int} \]

The wavefunction is now partially transformed into the Interaction picture

    \[\psi(t)=\psi_S(t)=e^{-{i\over \hbar}\hat{H}_0 t}\psi_I(t) \]

and so is H_1

    \[H_{1I}=e^{{i\over \hbar}\hat{H}_0 t} \, \hat{H}_{int} \, e^{-{i\over \hbar}\hat{H}_0 t}=-f(t) \, \sqrt{\frac{\hbar}{2m \omega}} \, \Big(\hat{a} \, e^{-i\omega t} +a^{\dagger} e^{i\omega t}\Big) \]

What is interesting about this picture is that the transformed wavefunction has time evolution entirely determined by \hat{H}_{int}

(4)   \begin{eqnarray*}\Big(\hat{H}_0+\hat{H}_{int}\Big)\psi_S(t)&=&i\hbar \frac{d}{dt}\psi_S(t) \nonumber\\ \Big(\hat{H}_0+\hat{H}_{int}\Big) e^{-{i\over \hbar}\hat{H}_0 t}\psi_I(t)&=&i\hbar \frac{d}{dt} \Big( e^{-{i\over \hbar}\hat{H}_0 t}\psi_I(t)\Big)\nonumber\\ &=&\hat{H}_0 \, e^{-{i\over \hbar}\hat{H}_0 t}\psi_I(t)+i\hbar e^{-{i\over \hbar}\hat{H}_0 t}{d\over dt}\psi_I(t)\nonumber\\ \Big(\hat{H}_{int}\Big) e^{-{i\over \hbar}\hat{H}_0 t}\psi_I(t)&=&i\hbar e^{-{i\over \hbar}\hat{H}_0 t}{d\over dt}\psi_I(t)\nonumber\\ e^{{i\over \hbar}\hat{H}_0 t}\Big(\hat{H}_{int}\Big) e^{-{i\over \hbar}\hat{H}_0 t}\psi_I(t)&=&i\hbar \, {d\over dt}\psi_I(t)\nonumber\\ \hat{H}_{int,I}\psi_I(t)&=& i\hbar {d\over dt}\psi_I(t)\end{eqnarray*}

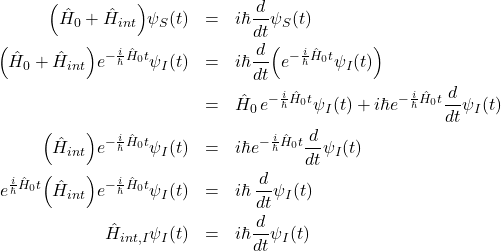
This can be formally integrated because we know its explicit time dependence,

    \[\psi_I(t)=\mathcal{T} \, e^{i\Big(\int_{-\infty}^t f(t')\sqrt{\frac{1}{2m\hbar\omega}}(\hat{a} \, e^{-i\omega t'} +\hat{a}^{\dagger} \, e^{i\omega t'})dt'\Big)} \, \psi_I(-\infty) \]

This form is very typical of what we see in quantum field theory, where we have powerful tools such as Wick’s theorem for evaluating such quantities. Wick’s theorem is based on the Baker-Campbell-Hausdorff relation, which we will use to exactly evaluate this operator. If the operator were any more complicated, we would need to expand it in a perturbation series.

Let

    \[F(\omega)=\sqrt{\frac{1}{2m\omega \hbar}}\int_{-\infty}^{\infty} f(t') \, e^{i\omega t'} dt' \]

and let t \rightarrow \infty,

    \[\label{eq:Ch10osc}\psi_I(t)=e^{i\Big(F(-\omega) \, \hat{a}+F(\omega) \, \hat{a}^{\dagger}\Big)} \, \psi_I(-\infty) \]

and if f(t)=f(-t), then F(\omega)=F(-\omega). The Baker-Campbell-Hausdorff relation says that for two operators \hat{A} and \hat{B} that obey [\hat{A},\hat{B}]=1

    \[e^{c(\hat{A}+\hat{B})}=e^{c \, \hat{A}} \, e^{c \, \hat{B}} \, \, e^{{c^2\over 2}}=e^{c \, \hat{B}} \, e^{c \, \hat{A}} \, \, e^{-{c^2\over 2}}\]

Recall our BCH relation:

    \[ e^{\hat{A}}e^{\hat{B}}=e^{\hat{A}+\hat{B}+{1\over 2}[\hat{A},\hat{B}]}\]

\noindent
Apply this with \hat{A}=\hat{a}^\dagger and \hat{B}=\hat{a};

    \[\psi_I(\infty)=e^{iF(\omega)(\hat{a}+\hat{a}^{\dagger})} \, \psi_I(-\infty)=e^{\frac{-F^2}{2}} \, e^{iF\hat{a}^{\dagger}} \, e^{iF\hat{a}} \, \psi_I(-\infty) \]

This is an extraordinary result, let the system be in the ground state in the remote past, since

    \[e^{iF\hat{a}}\psi_0=\psi_0, \qquad \hat{a}\psi_0=0\]

we find that after the force has been on for a long time it has excited the system, causing transitions into higher energy states

    \[\psi_I(\infty)=e^{\frac{-f^2}{2}}\sum_n \frac{(iF \hat{a}^{\dagger})^n}{n!} \psi_0=e^{\frac{-F^2}{2}}\sum_n\frac{(iF)^n}{n!} \, \sqrt{n!} \, \psi_n \]

using the action of the raising operator on the ground state. The probability that a measurement of the energy resulting in \hbar\omega(n+\frac{1}{2}) is then

    \[|\langle \psi_n|\psi_I(\infty)\rangle |^2=|e^{\frac{-F^2}{2}}\frac{(iF)^n}{\sqrt{n!}}|^2=e^{-F^2}\frac{F^{2n}}{n!} \]

which is a Poisson distribution whose peak value depends on the Fourier transform (frequency spectrum) of the applied force. This is an exact result.

Related Posts

Physics 7xx: Cosmic inflation-III, electric boogaloo
Protected: Phase operators in quantum theory?
Physics 7xx: Dynamic electric and magnetic fields-II
Home 2.0
error: Content is protected !!