Let ![]() be a random variable and
be a random variable and ![]() is expectation. Note that
is expectation. Note that ![]() is minimal when
is minimal when ![]()
![]()
and section 7.6 of Ross “A First Course in Probability” proves the important theorem
![]()
so that the left side is minimal when ![]() , implying that we can use the theorem to predict an outcome of
, implying that we can use the theorem to predict an outcome of ![]() subject an outcome of
subject an outcome of ![]() having occured, then the best guess for the outcome of
having occured, then the best guess for the outcome of ![]() is
is ![]() .
.
A nice example is afforded by problem 7.33; predict the number of rolls of a fair die necessary to roll a ![]() if on the first roll you got a
if on the first roll you got a ![]() , you will find that it is
, you will find that it is ![]() . This is because we are dealing with a geometric random variable, the probability of success on independent trial
. This is because we are dealing with a geometric random variable, the probability of success on independent trial ![]() with failures for trials
with failures for trials ![]() is
is
![]()
so the expected ![]() is
is ![]() , so if on the first roll we get a
, so if on the first roll we get a ![]() , we have to roll
, we have to roll ![]() more times before we expect to get a
more times before we expect to get a ![]() .
.
What is the best linear estimate of the next or expected ![]() ? Extremize
? Extremize
![]()
![]()
with respect to ![]() and
and ![]() , which results in
, which results in
![]()
![]()
or
![]()
which you may recall from teaching Physics 103, 201 or 207 lab are exactly the least-squares fit formulas for the best straight line fitting a collection of data. Therefore the best (linear) predictor of ![]() with respect to
with respect to ![]() is
is ![]() .
.
Example. German tank problem During WW-II (the Great Patriotic War) the Allies tried to estimate the number of German tanks from the knowledge that each had a unique serial number, which were sequential integers ![]() . From a sample size of
. From a sample size of ![]() captured/destroyed tanks and the largest serial number
captured/destroyed tanks and the largest serial number ![]() in the sample they tried to estimate
in the sample they tried to estimate ![]() , the largest serial number. They were able to do so quite accurately. We will need only the identity
, the largest serial number. They were able to do so quite accurately. We will need only the identity
![Rendered by QuickLaTeX.com \[\sum_{m=k}^N {m\choose k}={N+1\choose k+1}\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-c6fc60c55a39be6dbeba53851b946b14_l3.png)
which we prove by induction, it is true if ![]() ,
,
![Rendered by QuickLaTeX.com \[\sum_{m=k}^{N+1} {m\choose k}=\sum_{m=k}^{N} {m\choose k}+{N+1\choose k}={N+1\choose k+1}+{N+1\choose k}={N+2\choose k+1}\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-e535317e336534ee976754345bfa4dc7_l3.png)
Tanks are numbered ![]() . Sample
. Sample ![]() , the largest serial number in sample is
, the largest serial number in sample is ![]() , estimate
, estimate ![]() . Ansatz
. Ansatz
![]()
so conjecture that
![]()
Let ![]() be the random variable for the observed largest serial number observed,
be the random variable for the observed largest serial number observed, ![]() is the observed value. If we have a sample of size
is the observed value. If we have a sample of size ![]() , the smallest that the observed
, the smallest that the observed ![]() can be is
can be is ![]() (sample could have all of the lowest serial numbers
(sample could have all of the lowest serial numbers ![]() ), so that the range of
), so that the range of ![]() is
is ![]() . We find that
. We find that
![Rendered by QuickLaTeX.com \[\wp(X=m)={{m\choose k}-{m-1\choose k}\over {N\choose k}}={{m-1\choose k-1}\over {N\choose k}}\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-6e0c9c9c9daf3b02c18cc2f1812c8c34_l3.png)
Proof: If the largest is ![]() , then we must choose
, then we must choose ![]() other tanks n the sample from the
other tanks n the sample from the ![]() serial numbers lower than
serial numbers lower than ![]() , so
, so ![]() .
.
The expected value of ![]() is
is
![Rendered by QuickLaTeX.com \[E[X]=\sum_{m=k}^N m{{m-1\choose k-1}\over {N\choose k}}=\sum_{m=k}^N m{(m-1)!\over (k-1)!(m-k)!}{k!(N-k)!\over N!}\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-36d0b8eccaf44f42d7ca81ce9eb3d00b_l3.png)
![Rendered by QuickLaTeX.com \[={kk!(N-k)!\over N!}\sum_{m=k}^N{m\choose k}={kk!(N-k)!\over N!}{N+1\choose k+1}={k(N+1)\over k+1}\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-0ab18aedb30b71ad72712483e66380fa_l3.png)
Then
![]()
I would like to thank E. Basso for introducing this problem to me.
Unpredictability (the entropy or surprise)
The concept of “surprise” measures how surprised we would be if event ![]() occurred, and so is a measure of unpredicatbility. We have several axioms in its formulation
occurred, and so is a measure of unpredicatbility. We have several axioms in its formulation
![]()
![]() , we are not surprised that a sure thing occurs. Sure things are highly predictable.
, we are not surprised that a sure thing occurs. Sure things are highly predictable.
![]()
![]() strictly decreases with
strictly decreases with ![]() , we are more surprised when unlikely events occur.
, we are more surprised when unlikely events occur.
![]()
![]() is a continuous function of
is a continuous function of ![]() , so small
, so small ![]() -changes result in small
-changes result in small ![]() -changes.
-changes.
![]()
![]() , since if
, since if ![]() and
and ![]() and
and ![]() are independent events, then
are independent events, then ![]() .
. ![]() is the additional surprise from the knowledge that if told
is the additional surprise from the knowledge that if told ![]() has occurred, then told
has occurred, then told ![]() has occurred.
has occurred.
![]() The form that satisfies all axioms is
The form that satisfies all axioms is
![]()
Let ![]() have possible values
have possible values ![]() with probabilities
with probabilities ![]() .
.
\item The expected surprise upon learning the value of ![]() is
is
![]()
which is the information entropy of ![]() .
.
Example
A pair of fair dice are rolled. Let ![]() . Let
. Let ![]() be the value of the first dice. Compute
be the value of the first dice. Compute ![]() .
.
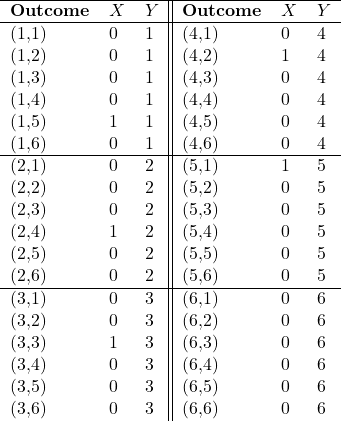
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Example
A coin with probability ![]() of coming up heads is flipped
of coming up heads is flipped ![]() times. Compute the entropy of the experiment.
times. Compute the entropy of the experiment.

Convert to ![]() by dividing by
by dividing by ![]() and sum the last column
and sum the last column
![]()
A lemma of great importance in statistical mechanics:
let ![]() and
and ![]() , then
, then
![]()
with equality occurring when each ![]() . This uses
. This uses ![]() for
for ![]() only and was used by Gibbs to prove maximality of the Boltzmann entropy.
only and was used by Gibbs to prove maximality of the Boltzmann entropy.
(1) 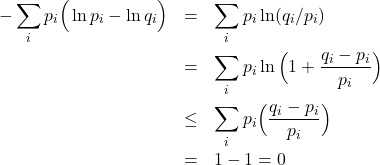
Uncertainty in a random variable (on average) decreases when a second random variable is measured. This makes intuitive sense (the second measurement reveals information about the first). Since entropy is a measure of the average surprise that you experience when ![]() is measured,
is measured, ![]() is a measure of the uncertainty in the value of
is a measure of the uncertainty in the value of ![]() . In other words
. In other words
![]()
We expand on the proof in Ross’s Chapter 9. Consider two sets of discrete variables ![]() :
:
![]()
![]()
then
(2) 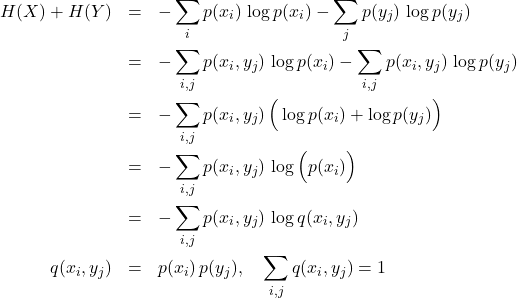
Lemma:
![]()
so we have
![]()
with equality when ![]() ,
, ![]() are independent. But we also have
are independent. But we also have
![]()
For a variable with two outcomes with probabilities ![]() and
and ![]()
![]()
is maximal when ![]() , which certainly erases any chances that you have of predicting the outcome, both outcomes are equally likely.
, which certainly erases any chances that you have of predicting the outcome, both outcomes are equally likely. ![]() for
for ![]() , and is zero by construction if
, and is zero by construction if ![]() since one or the other outcome is a sure thing. Gini impurity has the same properties
since one or the other outcome is a sure thing. Gini impurity has the same properties
![]()
For our two outcome case ![]() is maximal again at
is maximal again at ![]() and zero for sure bets
and zero for sure bets ![]() . Entropy and Gini impurity are both used for feature selection in the construction of tree classifiers.
. Entropy and Gini impurity are both used for feature selection in the construction of tree classifiers.