ML/AI: Probability and statistics-II. Discrete distributions

Binomial mass distribution
For a discrete random variable $X$ define the probability mass function

$p(a)=\wp(X=a)$

If $X$ can be only one of $\{x_1,x_2,\cdots, x_n\}$ then $p(x_i)\ge 0$ for $i=1,2,\cdots n$ and $p(x)=0$ if $x\ne x_i$ . We also must have $\sum_{i=1}^n p(x_i)=1$ .
A single Bernoulli random variable is one for which $p(1)=\wp$ (success) and $p(0)=1-\wp$ (failure).
We construct the generating function (in statistical physics this is the partition function)for multiple trials of a single Bernoulli process (such as shooting arrows at a bullseye) using $x$ as a simple place-holder or enumerator $x$

$G_1(x)=((1-p)+xp), \qquad G(1)=1$

and

${dG_1(1)\over dx}=p=\wp(success)$

Then since all trials are independent, all probabilities are multiplicative and

$G_n(x)=\Big((1-p)+xp\Big)^n=\sum_{m=0}^n x^m \wp(m\, \, success)$

$=\sum_m {n\choose m} p^m(1-p)^{n-m} x^m$

This should look very familiar; this is the binomial distribution. Note that in a generating function the coefficient of $x^m$ the the probability of event characterized by $m$ .

Bernoulli-binomial random variable. The Bernoulli random variable $i$ (a non-negative integer) is also called the binomial. Calling probability mass function $p(b)=\wp\{X=b\}$ , and $F(a)=\sum_{b\le a} p(b)$

$p(i)={n\choose i} \, p^i \, (1-p)^{n-i}$

gives the probability of $i$ successes and $n-i$ failures in $n$ independent trials with individual success probability $p$ . Note that (if $p<1-p$ )

$\sum_{i=0}^n p(i)=\sum_{i=0}^n {n\choose i} \, p^i \, (1-p)^{n-i}=(1-p)^n\sum_{i=0}^n {n\choose i} \, \Big({p\over 1-p}\Big)^i$

$=(1-p)^n\Big(1-{p\over 1-p}\Big)^n=1$

Example. An archer has a probability of making a bull’s eye of $1/3$ with each shot. What is her average score in a set of six shots?
The probability of $m$ bull’s eyes in the set is

$\wp(m)= {6\choose m} (1/3)^m(2/3)^{6-m}$

so her average will be

$\bar{m}=\sum_{m=0}^6 m \cdot \wp(m)= \sum_{m=0}^6 m \cdot{6\choose m} (1/3)^m(2/3)^{6-m}=2$

You can see that performing the sum $\bar{m}=\sum_m m\cdot\wp(m)$ could be mathematically difficult if $\wp(m)$ is complicated.
Example The probability that a given atom out of $N$ trapped in volume $V$ will be in subvolume $v$ is $p(1)=\wp=v/V$ , $p(0)=1-\wp=1-v/V$ . This was part of a qualifier problem.

Geometric random variable Consider independent trials, each with a success probability $\wp(1)=p$ , are performed until success occurs. $X$ is the number of trials required until success,

$\wp(X=n)=p(1-p)^{n-1}, \quad n=1,2,\cdots$

Note that

$\wp(X\ge n)=p\sum_{m=n}^\infty (1-p)^{m-1}=p\sum_{q=0}^\infty (1-p)^{n-1+q}$

$=p(1-p)^{n-1}\sum_{q=0}^\infty (1-p)^q=(1-p)^{n-1}$

$X$ is a geometric random variable. A distribution is memory-less if $\wp(X\ge n+m|X>m)=\wp(X\ge n)$ . The only distribution taking values in the positive integers that is memory-less is the geometric, since

$\wp(X\ge n+m|X>m)={\wp(X\ge n+m)\over \wp(X>m)}=\wp(X\ge n)$

$\wp(X\ge n+m)= \wp(X\ge n)\wp(X>m)$

and clearly $\wp(X\ge n)=(1-p)^{n-1}$ satisfies this.

Poisson random variable The Poisson variable $i$ (a non-negative integer) is

$p(i)={\lambda^i\over i!} \, e^{-\lambda}$

This is the limit of $n\rightarrow\infty$ and $p\rightarrow 0$ , $np=\lambda$ of the Bernoulli variable.
Consider the simplest experiment that can be conceived of; within a vanishingly small time interval $dt$ , a process either occurs (such as a nuclear decay), with probability $p$ , or does not, with probability $(1-p)$ . The probability $\wp(M)$ that within a macroscopic time $t=N \, dt$ , that $M$ such events occur, is generated by

$(pt +(1-p))^N =\phi(t)=\sum_{M=0}^N {N\choose M} p^M (1-p)^{N-M} \, t^M$

$=\sum_{M=0}^N \wp(M) \, t^M$

resulting in the binomial distribution

$\wp(M)={N\choose M} p^M (1-p)^{N-M}$

Notice that we say $\wp(M)$ rather than ${d\wp(M)\over dM}$ for a discrete distribution.
We call $\phi(t)=(pt +(1-p))^N$ the generating function of the distribution, which is very useful in obtaining moments.
The expectation or mean of this distribution is

$\mu=\sum_{M=0}^N M \, \wp(M) =\Big(\sum_{M=0}^N \wp(M) \, t^M\Big)_{t=1}$

$=\Big(t{d\over dt}\sum_{M=0}^N \wp(M) \, t^M\Big)_{t=1}$

$=t{d\over dt}\phi(t)\Big{|}_{t=1}=t \, p \, N (pt +(1-p))^{N-1}=p \, N$

This PDF has two important limits.
$\bullet$ First if we consider the case of $p\rightarrow 0$ but with $N\rightarrow\infty$ such that $pN=\mu$ remains constant, we get

$\lim_{p\rightarrow 0}\lim_{N\rightarrow\infty}(pt +(1-p))^N =\lim_{N\rightarrow\infty}(1+(t-1){\mu\over N})^N=e^{\mu t} e^{-\mu}$

and then

$\sum_{M=0}^\infty \wp(M) \, t^M=e^{\mu t} e^{-\mu}=\sum_{M=0}^\infty {\mu^M\over M!} e^{-\mu} \, t^M$

results in the Poisson distribution

$\wp(M)={\mu^M\over M!} e^{-\mu}=P(\mu, M)$

with parameter $\mu$ .
Example The probability that an ISP gets a call from a subscriber in any given hour is $0.01$ . The ISP has $300$ subscribers. What is the probability that the ISP will get $4$ calls in the next hour?
First we see that the most probable number of calls is

$\mu=(300)(0.01)=Np=3$

in an hour. Then

$\wp(4)={3^4\over 4}e^{-3}=0.168$

$\bullet$ The second important limit of the binomial theorem is used when we want to explore the region around the maximum value $\mu=np$ , which is the most probable value. We will expand the natural log of the distribution around $\mu=np$ by treating the discrete variable $M$ as if it were continuous, calling it $\xi$ for consistency with our previous examples;

$\ln \wp(\xi)=\ln \wp(\mu)+{d \ln \wp(\xi)\over d\xi}\Big{|}_{\xi=\mu}(\xi-np)$

$+{1\over 2}{d^2 \ln \wp(\xi)\over d \xi^2}\Big{|}_{\xi=\mu}(\xi-np)^2+\cdots$

however the second term vanishes since $\mu=np$ is an extreme point of the distribution. Take the logarithm of the probability

$\ln \wp(\xi)=\ln n! -\ln \xi! -\ln(n-\xi)! +\xi\ln p +(n-\xi)\ln(1-p)$

To evaluate the derivatives we use Stirling’s approximation

${d \ln \xi!\over d\xi}={d\over d\xi} (-\xi+\xi\ln \xi+\ln\sqrt{2\pi})=\ln \xi, \qquad {d^2 \ln \xi!\over d\xi^2}={1\over \xi}$

${d^2 \ln \xi!\over d\xi^2}\Big{|}_{\xi=np}={1\over np}$

and so

$\ln \wp(\xi)\approx \ln \wp(\mu) +{1\over 2}\Big(-{1\over \xi}-{1\over n-\xi}\Big)\Big{|}_{\xi=np}(\xi-np)^2+\cdots,$

$\wp(\xi)\approx \wp(\mu) \, e^{-{(\xi-np)^2\over 2np(1-p)}}$

which we can normalize via

$1=\int_{-\infty}^{\infty} \wp(\xi) \, d\xi, \qquad \wp(\xi)={1\over \sqrt{2\pi np(1-p)}} \, e^{-{(\xi-np)^2\over 2np(1-p)}}$

which we recognize as the Bell curve (the Normal distribution), peaked around $x=\mu=np$ with standard deviation $\sigma=\sqrt{np(1-p)}$ . Notice that the Maxwell-Boltzmann distribution is a normal distribution in velocity.
Fun fact: if $p<<1$ , then $\sigma=\sqrt{np(1-p)}\approx \sqrt{np}=\sqrt{\mu}$ .
Example (old format qualifier problem) A researcher performs counting of nuclear decays from a sample, making ten counts for ten seconds each, getting

$\{2,\quad 3, \quad 2,\quad ,4, \quad 1,\quad 2, \quad 5, \quad 3, \quad 1, \quad 2\}$

counts. For how many seconds should she count in order to measure the decay rate accurate to $5\%$ ?

Nuclear decays are Poissonian random deviates. We want to have ${\sigma\over \mu}={\sqrt{\mu}\over \mu}={1\over \sqrt{\mu}}=0.05$ , so we should count long enough so that the average number of counts gotten is ${1\over (0.05)^2}=400$ . We are getting ${2.5 \, counts \over 10 \, s}$ now, so we should count for ${2.5\over 10}={400\over T}$ , $T=1600 \, s$ .

Example (Gibbs distribution in Physics 415/715).
Let the universe $U$ consist of a system $s$ and a reservoir $r$ , so $U=s\bigcup r$ . The reservoir $r$ has $N_r$ boxes that can each hold $0$ or $1$ particle, and the system $s$ has $N_s$ such boxes. How many states does a universe containing $N<N_s+N_r$ particles have?
The number of ways that $N$ objects can be put into $N_s+N_r$ locations is

$\Omega(N)={N_s+N_r\choose N}={(N_s+N_r)!\over N!(N_s+N_r-N)!}$

which is the coefficient of $t^N$ in

$(1+t)^{N_r}(1+t)^{N_s}=(1+t)^{N_r+N_s}=\sum_{m=0}^{N_s+N_r}{N_s+N_r\choose m}t^m$

Carefully expand the left side;

$(1+t)^{N_r}(1+t)^{N_s}=\Big(\sum_{p=0}^{N_r}{N_r\choose p}t^p\Big)\Big(\sum_{q=0}^{N_s}{N_s\choose q}t^q\Big)$

$=\sum_{p,q}{N_r\choose p}{N_s\choose q}t^{p+q}$

By comparing these two expressions and picking out the coefficient of $t^N$ on each side we obtain

$\Omega(N)={(N_s+N_r)!\over N!(N_s+N_r-N)!}=\sum_{p+q=N}{N_r\choose p}{N_s\choose q}$

$=\sum_{q=0^N}{N_r\choose N-q}{N_s\choose q}=\sum_{q=0}^N \Omega_r(N-q)\Omega_s(q)$

where $\Omega_s(q)$ is the number of states of the system $s$ when populated with $q$ particles and $\Omega_r(N-q)$ is the number of states of the reservoir $r$ when populated with $N-q$ particles. These are mass functions since $N$ is a discrete variable, we would use ${d\Omega\over dN}$ if $N$ were continuous.

What is the probability that $s$ contains exactly $m$ particles?
This will be the ratio of the number of states with $m$ particles in $s$ and $N-m$ in $r$ to the total number of states

$\wp(m)={{N_r\choose N-m}{N_s\choose m}\over {N_s+N_r\choose N}}$

The Boltzmann entropy of the system containing $m$ particles is $S=k\ln\wp(m)$ , and {\bf Boltzmann’s maximal entropy principle} says that the equilibrium population $m$ is the most probable. Use Stirling’s formula to evaluate this: maximize the entropy with respect to $m$

$S=-k_B\ln \wp, \qquad 0=\ln\Big({N_s-m\over m}\Big)-\ln\Big({N_r-N+m\over N-m}\Big)$

taking anti-logs

${N_s\over m}-1={N_r\over N-m}-1, \qquad {m\over N_s}=\rho_s={N-m\over N_r}=\rho_r$

we obtain the result that the most likely distribution of particles between system $s$ and reservoir $r$ is the one that makes their {\bf densities} $\rho_r$ and $\rho_s$ equal! Define the {\bf chemical potential}

$-\mu=T\Big({\partial S\over \partial m}\Big)$

which represents the work needed to move a particle from $r$ to $s$ when $r$ and $s$ are in thermal and matter equilibrium, and $r$ is at temperature $T$ . Then for $s$

$-{\mu_s\over T}=k \ln\Big({N_s-m\over m}\Big)=k\ln\Big({1\over \rho_s}-1\Big)$

$\rho_s={1\over e^{-\mu_s/kT}+1}$

This is an interesting and exact result. Notice that the equilibrium condition says equilibrium between $r$ and $s$ occurs when

$\mu_r=\mu_s$

then there is no energy cost to move particles from $r$ to $s$ . Another observation is that if $\mu_s<0$ , then the density of $s$ (the number of particles in $s$ ) is low. Under those conditions matter would migrate from $r$ into $s$ until $\rho_r=\rho_s$ , matter migrates from high to low $\mu$ .

Stirling’s approximation
The gamma function is an analytic continuation of the factorial to non-integer values

$\Gamma(s)=\int_0^\infty e^{-x} \, x^{s-1} \, dx$

If $s=n>0$ an integer, then $\Gamma(n)=(n-1)!$ , which is easy to prove by integration by parts or by induction.
Recall

$I=\int_{-\infty}^\infty e^{-a x^2} \, dx=\sqrt{{\pi\over a}},$

$\Gamma(s)=\int_0^\infty e^{-x+(s-1) \, \ln x} \, dx=\int_0^\infty e^{-f(x)} \, dx$

find the $x$ -value $x_*$ that makes $f(x)$ minimal, it contributes the most to the integral, and expand $f$ around it

$f(x)=f(x_*)+(x-x_*) \, f'(x_*)+{1\over 2} (x-x_*)^2 \, f''(x_*)+\cdots$

$=f(x_*)+{1\over 2} (x-x_*)^2 \, f''(x_*)+\cdots$

put this back into $\Gamma(s)$ , and use the integral $I$ to obtain an approximate formula for $\Gamma(s)$

$\Gamma(s)=(s-1)!\approx \sqrt{2\pi} \, s^{s-{1\over 2}} \, e^{-s}$

when $s$ is very large. Finally you will need to use

$\int_0^\infty G(x-x_*) \, dx=\int_{-x_*}^\infty G(y) \, dy\approx \int_{-\infty}^\infty G(y) \, dy$

for $x_*$ very large.

Cumulants
Let $\{X\}$ denote an event $X$ . Cumulative distribution function

$F(b)=\wp\{X\le b\}$

is non-decreasing, approaches $0$ for $b\rightarrow -\infty$ and $1$ for $b\rightarrow \infty$ and is right-continuous

$\lim_{\delta\rightarrow 0}F(b+\delta)=F(b), \qquad \delta \ge 0$

Note that

$\{X\le b\}=\{X\le a\}\cup\{a<X\le b\}\implies \wp\{X\le b\}$

$=\wp\{X\le a\}+\wp\{a<X\le b\}$

$\wp\{a<X\le b\}=F(b)-F(a)$

and calculation that $X<b$ is a simple limit

$\wp\{X<b\}=\lim_{n\rightarrow \infty}\wp\{-\infty<X\le b-{1\over n}\}$

$=\lim_{n\rightarrow \infty}\Big(F(b-{1\over n})-F(-\infty)\Big)=\lim_{n\rightarrow \infty}F(b-{1\over n})$

Example (Problem 4.1)
Two balls are randomly chosen from an urn containing 8 white, 4 black and 2 orange balls. You win $1$ dollar for each black, and lose $1$ dollar for each white selected. Let $X$ denote your winnings. What are the possible values of $X$ , and find the mass function for the distribution of this variable.
Probability of $2$ white (-2): $\wp(2w)=\Big({8\over 14}\Big)\Big({7\over 14}\Big)={28\over 91}$ , probability of $2$ black (4): $\wp(2b)=\Big({4\over 14}\Big)\Big({3\over 14}\Big)={6\over 91}$ , probability of $1$ white no black (-1): $\wp(1w0b)={2\choose 1}\Big({8\over 14}\Big)\Big({2\over 14}\Big)={16\over 91}$ , probability of $1$ black no white (2): $\wp(0w1b)={2\choose 1}\Big({4\over 14}\Big)\Big({2\over 14}\Big)={8\over 91}$ , probability of no white no black (0): $\wp(0w0b)=\Big({2\over 14}\Big)\Big({1\over 14}\Big)={1\over 91}$ , probability of $1$ white $1$ black (1): $\wp(1w1b)={2\choose 1}\Big({8\over 14}\Big)\Big({4\over 14}\Big)={32\over 91}$ .
Example
Two fair dice are rolled. Let $X$ equal the product of the values. Compute $\wp(X=i)$ for each $i$ .

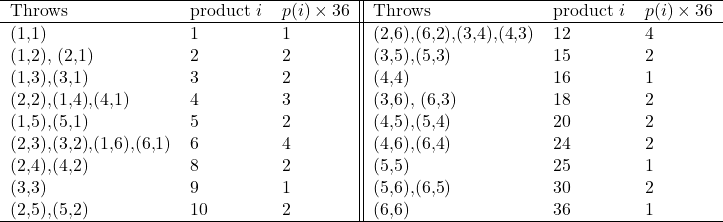
Example
Suppose that the number of accidents occurring on a highway each day is a Poisson random variable with parameter $\lambda=3$ .
A. Find the probability of 3 or more accidents per day.
B. Find the probability of 3 or more accidents per day provided at least one accident has occurred.

$\wp(3)={3^3\over 3!} e^{-3}, \quad \wp\{X\ge 3\}=1-\wp\{X\le 2\}=1-\Big({3^0\over 0!}e^{-3}+{3^1\over 1!}e^{-3}+{3^2\over 2!}e^{-3}\Big)$

$1-{17\over 2}e^{-3}$

Let $E$ be the even of $3$ or more accidents, and $F$ the event of $1$ or more accidents

$\wp(E)=1-{17\over 2}e^{-3}=\wp(EF), \qquad \wp(F)=1-\wp(0)=1-e^{-3}$

$\wp(E|F)={\wp(EF)\over \wp(F)}={1-{17\over 2}e^{-3}\over 1-e^{-3}}$

Example
If you buy a lottery ticket in $50$ lotteries, in each of which your chances of winning a prize is ${1\over 100}$ , what is the probability that you will win a prize at least once, exactly once, at east twice?
This is the limit of a binomial (Bernoulli) random number; many trials each with small probability

$\wp(i \, wins)={50\choose i}\Big({1\over 100}\Big)^i\Big(1-{1\over 100}\Big)^{50-i}$

$\rightarrow {\lambda^i\over i!}e^{-\lambda}, \qquad \lambda=(50)({1\over 100})={1\over 2}$

$\wp(i\ge 1)=1-\wp(0)=1-{(1/2)^0\over 0!} e^{-1/2}=1-e^{-1/2}$

$\wp(1)={(1/2)^1\over 1!} e^{-1/2}={e^{-1/2}\over 2}$

$\wp(i\ge 2)-1-\wp(0)-\wp(1)=1-{e^{-1/2}\over 2!}-{(1/2)^0\over 0} e^{-1/2}=1-{3\over 2}e^{-1/2}$

Example
From the generic grand canonical partition function for identical particles with single-particle partition functions $Z$ determine the distribution function for the number of particles $n$ in the system when in equilibrium with a heat and particle reservoir. What is $\langle n\rangle$ , the average value?