Physics 7xx: Useful integrals and how to perform them

I will use complex variables to show you how to do these integrals. If you don’t know these methods, you can simply use the results. If you want to learn the methods, they are not difficult, and they are very rewarding. An inexpensive addition to your library would be ” Complex Analysis with Applications” (Dover) by Robert Silverman.
You are all very familiar with

$I_1=\int_{-\infty}^\infty e^{-ax^2} \, dx=\sqrt{{\pi\over a}}$

and

$I_{n+1}=\int_{-\infty}^\infty x^{2n} \, e^{-ax^2} \, dx=(-1)^n {d^n\over da^n}I_1={(2n-1)!!\over 2^n}\sqrt{{\pi\over a^{2n+1}}}$

with $(2n-1)!!=(2n-1)\cdot(2n-3)\cdots 5\cdot 3\cdot 1$ .

Use the fact that the exponential function is holomorphic, consequently $\oint_C e^{\pm az^2} \, dz=0$ for any closed curve $C$ in a simply connected open subset of $\mathbb{C}$ (Cauchy’s theorem)
to evaluate (with $a>0$ real)

$I_i(R)=\oint_C e^{i a z^2}=0$

on the path $C$ shown, in which $R\rightarrow\infty$ . Break the path $C$ into three parts for which $z=x$ , $z=R(\cos\theta+i\sin\theta)$ , and $z=r(\cos(\pi/4)+i\sin(\pi/4))$
with $0\le \theta\le \pi/4$ , $0\le x\le R$ and $r\le 0\le R$ and explicitly compute $I_i$ in the limit as $R\rightarrow\infty$ .
Obtain an explicit expression for ( $a$ is real)

$J_i=\int_0^\infty e^{-iax^2} \, dx$

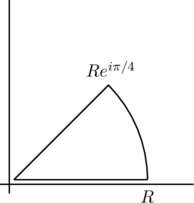
We notice that the integrand has no singularities within $C$ , so

(1) $\begin{eqnarray*}0&=&I_i(R)=\oint_C e^{i a z^2}\nonumber\\ &=&\int_0^R e^{-iax^2} \, dx+\int_0^{\pi/4} e^{ia (R\cos\theta+iR\sin\theta)^2} iR e^{i\theta} d\theta\nonumber\\ &+&\int_R^0 e^{iar^2(\cos(\pi/4)+i\sin(\pi/4))^2} (\cos(\pi/4)+i\sin(\pi/4)))\, dr\nonumber\\ &=& \int_0^R e^{-iax^2} \, dx+0-{(1+i)\over \sqrt{2}}\int_0^R e^{ia(ir^2)}\nonumber\nonumber\end{eqnarray*}$

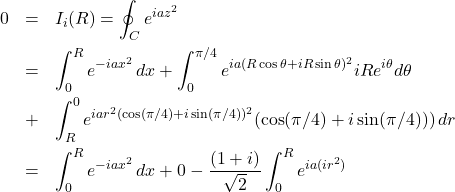
(the second integral on the second line has exponent

$i R^2(e^{i\theta})^2=iaR^2\cos(2\theta)-aR^2 \sin(2\theta)\rightarrow -\infty, \qquad R\rightarrow\infty$

and so vanishes in the limit. Now let $R\rightarrow \infty$

$\int_0^\infty e^{-iax^2} \, dx={(1+i)\over \sqrt{2}}\int_0^\infty e^{ia(ir^2)}={(1+i)\over \sqrt{2}}{1\over 2}\sqrt{{\pi\over a}}$

You are all familiar with

$I_2=\int_{-\infty}^\infty e^{-ax^2+bx}dx=\sqrt{{\pi\over a}} \, e^{{b^2\over 4a}}, \quad a\in \mathbb{R}_$

which you obtain by the variable change $x\rightarrow x-{b\over 2a}$ and completing the square. This does not change the path of integration. But what about

$I'_2=\int_{-\infty}^\infty e^{-ax^2+ibx}dx$

The same transformation changes the path of integration to a line in the complex plane parallel to the real axis.

The correct way to evaluate the integral is by contours, consider that

$\oint_C e^{-a z^2 +ibz}=0$

integrated over the illustrated contour, in the limit $L\rightarrow \infty$ .

$\oint_C e^{-a z^2 +ibz}=0=I_2+\int_{\infty}^{-\infty} e^{-a(x-iv)^2+ib(x-iv)} \, dx$

and the choice $v=-{b\over 2a}$ turns this into

$I'_2=e^{-{b^2\over 4a}} \, \int_{-\infty}^{\infty} e^{-ax^2} \, dx=e^{-{b^2\over 4a}}\sqrt{{\pi\over a}}$

The contributions from the two vertical segments will be zero

$\lim_{L\rightarrow \infty}\int_0^{-v} e^{-a(L+iy)^2+ib(L+iy)} i \, dy=\lim_{L\rightarrow \infty}e^{-aL^2+ibL}\int_0^{-v} e^{-a(2iLy-y^2)-by} i \, dy=0$

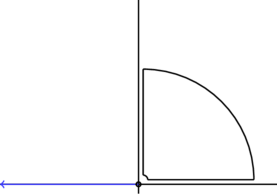
Let’s show that

$I_3=\int_0^\infty x^a e^{ix}dx$

for $a>0$ is just a Gamma function. Evaluate $\oint_C z^a e^{iz}dz=0$ on this contour. Since $a$ need not be integral, we have a cut, which I draw from the origin to infinity and stretch out along the negative real axis (you can place it anywhere).

(2) $\begin{eqnarray*}\oint_C z^a e^{iz}dz=0&=&\int_r^Rx^a e^{ix}dx+\int_{0}^{\pi/2}(Re^{i\theta})^a e^{iR(\cos\theta+i\sin\theta)} iRd^{i\theta}d\theta\nonumber\\ &+&\int_R^r(iy)^a e^{i(iy)}\, idy+\int_{\pi/2}^{0}(re^{i\theta})^a e^{ir(\cos\theta+i\sin\theta)} ird^{i\theta}d\theta\nonumber\end{eqnarray*}$

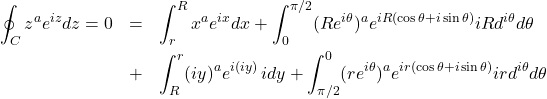
and we let $r\rightarrow 0$ and $R\rightarrow \infty$ . Hopefully you see that the integrals over the arcs vanish,

$\int_0^\infty x^a e^{ix}dx=i^{a+1}\int_0^\infty y^a e^{-y}\, dy=i^{a+1}\Gamma(a+1)$

and we can analytically continue this integral to negative non-integral $a$ using the Gamma function functional relation.

Asymptotic formulas
In many applications we will need to evaluate integrals such as

$I_1(x_0)=\int_{-x_0}^{x_0} e^{-ax^2} \, dx$

in which $x_0>>1$ but is not infinite. What we will most often do is simply say that $I_1(x_0)\approx I_1(\infty)$ , but we may need to know how significant the error is when we make this approximation.
Integration by parts repeatedly gives you

$\int_{x_0}^\infty e^{-x^2} \, dx=e^{-x_0^2}\Big({1\over 2x_0}-{1\over 4x_0^3}+{3\over 8x_0^5}+\cdots\Big)$

and the error is exponentially small

$\int_{-x_0}^{x_0} e^{-x^2} \, dx=I_1(\infty)-e^{-x_0^2}\Big({1\over 2x_0}-{1\over 4x_0^3}+{3\over 8x_0^5}+\cdots\Big)$

We will make heavy use of approximations to $n!$ , which we will obtain from

$n!=\Gamma(n+1)=\int_0^\infty e^{-x} \, x^n \, dx$

A standard method for evaluating

$\int_0^\infty G(x) \, x^n \, dx, \qquad n>>1$

is to find the point $x_0$ where $E(x)=\ln G(x)-n\ln x$ is maximal, and rewrite as

$E(x)=E(x_0)+{1\over 2}(x-x_0)^2 E''(x_0)+\cdots$

and perform the integration; if $E''(x_0)<0$ we have

$\int_0^\infty G(x) \, x^n \, dx\approx e^{E(x_0)}\int_{-x_0}^\infty e^{-{|E''(x_0)|\over 2}x^2+{1\over 3!}E'''(x_0)x^3+\cdots } \, dx\approx e^{E(x_0)}\Big(\sqrt{{2\pi\over |E''(x_0)|}}+\cdots\Big)$

replacing $x_0$ with $-\infty$ if appropriate.
For our case we obtain Stirling’s approximation

$n!\approx \sqrt{2\pi n} \, n^n \, e^{-n}, \qquad n>>1$

and Stirling’s approximation begets the following very useful (for paramagnetic and polymeric models) expression

${1\over 2^n}{n \choose {n\over 2}-x}={1\over 2^n}{n!\over ({n\over 2}-x)!({n\over 2}+x)!}$

$\approx \sqrt{{2\over \pi n}} \, e^{-2x^2/n}, \qquad n>>1$

This technique is known as the saddle-point method.

Home 2.0

Physics 7xx: Useful integrals and how to perform them

Related Posts

Physics 7xx: Useful integrals and how to perform them

Published by Jeff on November 30, 2021November 30, 2021

Related Posts

Protected: 711. Lecture 2

Protected: Physics 711: Lecture 32

Protected: Physics 711: PS-7 solutions