Physics 715: Generating functions, partition functions, and Legendre transformations

Let’s re-examine the maximal entropy principle ( an earlier post) from a probablistic point of view (se the post on ML/AI-probability-I for use of generating functions to count states), starting with

$\Omega(N,V,E)=\sum'_\mu1\quad \mbox{$\Omega=$ sum over the microstates}$

where we sum over identifiers of microstates that result in the same macrostate. Divide

$1=\sum'_\mu {1\over \Omega(N,V,E)}$

which we interpret as stating that the probability that you reach into an ensemble of systems in macrostate $N,V,E$ and pull out a system whose microstate is $\mu$ .

$\wp(\mu)={1\over \Omega(N,V,E)}$

The maximal entropy principle is a maximal probability principle, the most likely macrostate is the equilibrium macrostate. We maximize the probability that the entire universe is in a given macrostate ( $u=s\cup\overline{s}\approx\overline{s}$ )

$1=\sum_{E_s}\sum_{N_s}\sum_{V_s} {\Omega_s(N_s,V_s,E_s)\Omega_{\overline{S}}(N-N_s, V-V_s,E-E_s)\over \Omega_{u}(N, V,E)}$

$\wp(N_s,V_s,E_s)={\Omega_s(N_s,V_s,E_s)\Omega_{u}(N-N_s, V-V_s,E-E_s)\over \Omega_{\overline{S}}(N, V,E)}$

Restrict our attention to energy only, and we suppose that $E=N\bar{E}$

${\Omega_{\overline{S}}(E-E_s)\over \Omega_{\overline{S}}(E)}\approx \Big(1-{E_s\over N\bar{E}}\Big)^N\approx e^{-E_s/E}=t^{E_s}$

And so a generating function is born! The un-normalized probabilities we write as

$Z(t)=\sum_{E_s}\Omega_s(E_s) \, t^{E_s}$

The probability that $s$ has $E_s$ is

$\wp(E_s)={\Omega_s(E_s) \, t^{E_s}\over Z(t)}$

and the equilibrium partition of energy is that which maximizes the probability

$0={d\Omega_s\over dE_s} \, t^{E_s}+\Omega_s \ln t \, t^{E_s}, \qquad {d\ln\Omega_s\over dE_s}=-\ln t$

which brings us back to the First law, compatibility requires $-\ln t=\beta=1/kT$ .
Multiply this equation by $dE_s$ and use the first law; when $E_s$ is the equilibrium energy of $s$ ;

${1\over k} dS_s-{dE_s\over kT}=0, \qquad 0=dE_s-TdS_s$

which we recognize is the $F$ -theorem (since we have held $V,T$ constant)

$dF=0=dE-T dS$

is the equilibrium condition for constant $V$ and constant $T$ .
In summary, here is the interpretation; create a new generating function by introducing an intensive variable $t$ . It is intensive because it has nothing to do with $s$ , it has everything to do with $\overline{s}$ . The new generating function is a re-expression of the summed probabilities that $s$ is in a certain macrostate when in contact with $\overline{s}$ . Maximizing that probability will give you equilibrium values of extensive properties of $s$ .

While we are on this subject let’s show that the transformation from one thermodynamic potential

$E(S,V,N)\rightarrow F(T,V,N)\rightarrow \left\{\begin{array}{l} G(T,P,N)\\J(T,V,\mu)\end{array}\right. \cdots$

by Legendre transformation

$F=E-TS, \quad T=\Big({\partial E\over \partial S}\Big)_{V,N}, \qquad G=F+PV, \quad P=-\Big({\partial F\over \partial V}\Big)_{T,N}$

is paralleled in statistical mechanics by Laplace transformation of partition/generating functions. Starting with the generating function $\Omega(E,V,N)$ , $\Omega=e^{S(E,V,N)/k_B}$ we have seen that

$Z[T,V,N]=\int \Omega(E,V,N) e^{-E/k_BT} \, dE=\int e^{S(E,V,N)/k_B} e^{-E/k_BT} \, dE$

$=e^{-F/k_BT}\, \int e^{-{(E-E_*)^22\over 2k_BT^2C_V}+\cdots} dE$

and in the thermodynamic limit

$-k_B T\ln Z=F_*$

in which $F=F_*$ computed at the most probable (equilibrium) energy of the system in equilibrium with the reservoir.
Let’s quickly review the transformation at the potential/thermodynamic level. Start with the definition of extensive energy

$E=E(S,V,N), \qquad E(\lambda S,\lambda V, \lambda N)=\lambda E(S,V,N)$

Differentiate with respect to $\lambda$ and set $\lambda=1$

$S\Big({\partial E\over \partial S}\Big)_{V,N}+V\Big({\partial E\over \partial V}\Big)_{S,N}$

$+N\Big({\partial E\over \partial N}\Big)_{S,V}=E(S,V,N)$

Use the first law

$dE=T dS-P dV+\mu dN, \quad T=\Big({\partial E\over \partial S}\Big)_{V,N}$

$-P=\Big({\partial E\over \partial V}\Big)_{S,N}, \quad \mu=\Big({\partial E\over \partial N}\Big)_{S,V}$

to arrive at the Gibbs-Duhem relation

$E=E(S,V,N)=TS-PV+\mu N$

Let

$F=F(T,V,N)=E-TS$

$dF=dE-T dS-S dT=-S dT-P dV+\mu dN$

and finally introduce the grand potential

$J=F-\mu N, \qquad dJ=-S dT-P dV-N \, d\mu$

for which

$-S=\Big({\partial J\over \partial T}\Big)_{V,\mu}, \qquad -P=\Big({\partial J\over \partial V}\Big)_{T,\mu}$

$-N=\Big({\partial J\over \partial\mu}\Big)_{T,V}$

Let’s create another Laplace transform of $Z$

$Q[T,V,\mu]=\sum_N Z[T,V,N] e^{\beta \mu N}, \qquad \beta=1/k_B T$

Calling $e^{\beta \mu}=t$ we see that this can be used as a generating function counting variable in the absence of energetics. Think of this as

$Q[T,V,\mu]=\int Z[T,V,N] e^{\beta \mu N} dN=\int e^{-(F-\mu N)/k_B T} \, dN$

and expand around the equilibrium system occupancy $N_*$ holding $V,T$ fixed

$F(N)-\mu N=F(N_*)+\Big({\partial F\over \partial N}\Big)_*(N-N_*)$

$+{1\over 2}\Big({\partial^2 F\over \partial N^2}\Big)_*(N-N_*)^2+\cdots -\mu N$

$=F(N_*)+\mu(N-N_*)+{1\over 2}\Big({\partial \mu\over \partial N}\Big)_*(N-N_*)^2+\cdots -\mu N$

To evaluate $\Big({\partial \mu\over \partial N}\Big)_{V,T}$ use Gibbs-Duhem

$0=-S dT+V dP-N \, d\mu$

$N\Big({\partial \mu\over \partial N}\Big)_{V,T}=-S\Big({\partial T\over \partial N}\Big)_{V,T}+V\Big({\partial P\over \partial N}\Big)_{V,T}$

$=V\Big({\partial P\over \partial N}\Big)_{V,T}$

and the triple-product identity, and the isothermal compressibility $k_T=-{1\over V}\Big({\partial V\over \partial P}\Big)_T$

$\Big({\partial P\over \partial N}\Big)_{V,T}\Big({\partial N\over \partial V}\Big)_{P,T}\Big({\partial V\over \partial P}\Big)_{N,T}=-1$

$=\Big({\partial P\over \partial N}\Big)_{V,T}\Big({N\over V}\Big)\Big(-Vk_T\Big)$

$\Big({\partial P\over \partial N}\Big)_{V,T}={1\over N k_T}, \qquad \Big({\partial \mu\over \partial N}\Big)_{V,T}={V\over N^2 k_T}$

$Q[T,V,\mu]=\int e^{-{1\over k_BT}\Big(F_*-\mu N_*+{V(N-N_*)^2\over 2N_*^2k_T}+\cdots\Big)} \, dN$

$\langle (N-N_*)^2\rangle=2N_*^2k_Tk_BT/V$

Integrate, take logs, remember $\ln Q$ and $F$ and $J\propto N$ , $T\,k_T$ are intensive, and $V\propto N$ , so in the thermodynamic limit

$J=F-\mu N$

$=-k_BT\ln Q-k_BT\ln\sqrt{2\pi N_*^2k_Tk_BT/V}\rightarrow J=-k_BT\ln Q$

Example. Consider our gas of $n$ particles in a box of volume $V$ for which $\omega(n,V)={V+n-1\choose n}=Z$ . Then

$Q=\sum_nZ[n,V] e^{\beta\mu n}=\sum_n {V+n-1\choose n} e^{\beta\mu n}=(1-e^{\beta\mu})^{-V}$

(in which you recognize the generating function if we call $t=e^{\beta \mu}$ ). The results for the average system occupancy when in chemical/matter equilibrium with a particle reservoir looks very Bose-Einsteinish

$N_*=-\Big({\partial J\over \partial\mu}\Big)_{T,V}={V\over e^{-\beta\mu}-1}$

Example $Q$ for noninteracting lattice gases of $V$ cells can be constructed from the requirement that $J$ is extensive, the entire gas is simply $V$ copies of a single cell lattice gas, and the cells are distinguishable by position in the lattice, so $Q=(Q_1)^V$ where $Q$ is the grand canonical partition function of a single cell, therefore $J=-PV=-k_BT\ln Q=-k_BTV\ln Q_1$ . For a single cell with occupancies $n$ by identical particles there is one way to put $n$ particles in a cell, so $Q_1=\sum_n 1\cdot e^{-\beta E(n)}e^{\beta\mu n}=\sum_n e^{-\beta E(n)}z^n$ where $E(n)$ is the energy of the cell containing $n$ particles. For example if $n=0,1$ are the allowed occupances and there is a binding energy $-\epsilon$ then $Q_1=1+e^{\beta\epsilon}z$ and $Q=(1+e^{\beta\epsilon}z)^V$ for the entire system. The equation of state is gotten by eliminating $z$ between

$\bar{n}=-\Big({\partial J\over \partial \mu}\Big)_{T,V}=z\Big({\partial \ln Q\over \partial z}\Big)_{T,V}, \quad \mbox{and}\quad P=k_BT\ln Q$

In thermodynamics we obtain everything from a potential and the first law. In statistical physics we obtain everything from a partition (generating) function correlated with a potential.
Sometimes the variables that appear in $Z[T,V,N]$ may not be the most convenient for some types of calculations, suppose that we need to use $P$ , $T$ , and $N$ as the independent variables? We transform into this set using Legendre transformations in classical thermodynamics. For example we know that

$F=F(T,V,N)\qquad\mbox{and}\qquad dF=-S dT-P dV+\mu dN$

we could convert to a new potential\index{Legendre transformation}

$G=G(P,T,N)=F+PV=\mu N$

differentiate

$dG=dF+P dV+V dP=-S dT+V dP+\mu dN, \qquad \mbox{for which}$

$-S=\Big(\frac{\partial G}{\partial T}\Big)_V, \qquad V=\Big(\frac{\partial G}{\partial P}\Big)_T$

How do we accomplish the same transformation in the statistical mechanics context?
We do it with Laplace transformation to a new generating function

$Y(T,P,N)=\int_0^{\infty}e^{\frac{-PV}{kT}}Z(T,V,N) \, dV$

Let’s demonstrate again that this is equivalent to the transformation

$G=F+PV, \qquad \mbox{with}\qquad G(T,P,N)=-kT\ln Y(T,P,N)$

To do this expand $\ln Z=-{1\over k_B T} F$ about the most probable volume for the system (hold $T$ fixed)

(1) $\begin{eqnarray*}F(V)&=&V(V_*)+(V-V_*)\Big(\frac{\partial F}{\partial V}\Big)_*+\frac{1}{2}(V-V_*)^2\Big(\frac{\partial^2 F}{\partial V^2}\Big)_*+\cdots\nonumber\\ \Big(\frac{\partial F}{\partial V}\Big)_*&=&-P\nonumber\\ \Big(\frac{\partial^2 F}{\partial V^2}\Big)_*&=&-\Big({\partial P\over \partial V}\Big)_T={1\over V_* k_T}\nonumber\end{eqnarray*}$

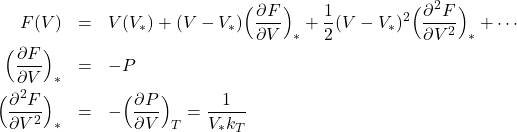
this allows us to write

(2) $\begin{eqnarray*}Y&=&Z(V_*,T)\int_0^{\infty} e^{-\frac{PV}{k_BT}}e^{\frac{P(V-V_*)}{k_BT}}e^{-\frac{(V-V_*)^2}{2V_* k_Tk_BT}}\cdots dV\nonumber\\ &=&Z(V_*,T)e^{-\frac{PV_*}{k_BT}}\int_0^{\infty} e^{-\frac{(V-V_*)^2}{2V_* k_Tk_BT}}\cdots dV\nonumber\end{eqnarray*}$

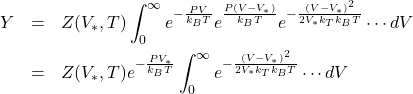
take logs of both sides and multiply by $kT$ ;

$-kT \ln Y=PV_*-kT\ln Z+kT\ln\Big(\int e^{-\frac{(V-V_*)^2}{2V_* k_T k_BT}}dV\Big)$

$\langle(V-V_*)^2\rangle=2V_*k_T k_BT$

the quantity $k_BT$ is of the same order as $PV$ , but the integral is Gaussian and is of the order of $\sqrt{N}\sim\sqrt{V_*}$ , and $\ln N<<N$ , so in the thermodynamic limit we obtain an extensive function $-k_BT\ln Y$ .

$-kT\ln Y=PV_*+F\equiv G$

Therefore we learn that the process of hopping from one thermodynamic potential in thermodynamics is implemented at the statistical mechanical level by Laplace transforming one partition function to get a new one.
Notice that we have been able to write all of the state distribution functions as normal distribution functions with variances given by thermodynamical quantities.

Home 2.0

Physics 715: Generating functions, partition functions, and Legendre transformations

Related Posts

Physics 715: Generating functions, partition functions, and Legendre transformations

Published by Jeff on November 30, 2021November 30, 2021

Related Posts

Protected: GRE-prep: Faraday’s law and displacement current problems

Protected: GRE-prep: Thermodynamics problems-II

Protected: GRE-prep: Optics