Physics 7xx: Complex variables-1. Riemann surfaces

In order to understand integration in the complex plane (and integration in general) one of the few necessities will be a need to rethink what is meant by the domain and range of functions of a complex variable. The domain $\mathcal{D}$ of a function, also called its support, is the set of $z$ values for which $f(z)$ is defined. The range is the set of all $f(z)$ for $z\in \mathcal{D}$ .
We will not encounter any problems with the trigonometric and hyperbolic functions, and so we will look at these first. These functions are best built from the exponential, which for a complex argument holds no surprises;

$e^z=e^{x+iy}=e^x \, e^{iy}=e^x \, \Big(\cos y +i\sin y\Big)$

by use of the Euler identity, which we have seen repeatedly. We can use this to illustrate some facts that have been difficult to prove by other means, namely De Moivre’s theorem

$e^{inx}=\cos nx +i \, \sin nx=(e^{ix})^n=(\cos x+i \, \sin x)^n$

which gives us a very nice polar representation of a complex number

$x+iy=\sqrt{x^2+y^2} \big({x\over \sqrt{x^2+y^2}}+i{y\over \sqrt{x^2+y^2}}\big)=r \, (\cos\theta+i \, \sin\theta)=r \, e^{i\theta}$

with $\tan\theta={y\over x}$ .

Consider the sine of a complex number

$\sin z=\sin(x+iy)=\sin x \, \cos iy + \, \cos x \, \sin iy$

we can use Euler

$\sin z={e^{iz}-e^{-iz}\over 2i}, \qquad \cos z={e^{iz}+e^{-iz}\over 2}$

to obtain

$\sin iy={e^{i^2y}-e^{-i^2y}\over 2i}={1\over i}{e^{-y}-e^y\over 2}=i \, \sinh y$

and

$\cos iy=\cosh y$

and we arrive at a real-imaginary part decomposition of the sine of a complex number

$\sin z=\sin(x+iy)=\sin x \, \cosh y + i \, \cos x \, \sinh y$

and it is easy to verify by similar means that

$\cos z=\cos(x+iy)=\cos x \, \cosh y - i \, \sin x \, \sinh y$

there are no great surprises here.

The log function is another story. Consider that $\ln xy=\ln x + \ln y$ and take the log of $z$

$\ln z=\ln(x+iy)=\ln(r e^{i\theta})=\ln r +i \theta$

$\ln (x+iy)=\ln \sqrt{x^2+y^2}+i \tan^{-1}{y\over x}$

So far so good, but close examination shows us what we have jumped into. Remember that

$e^{i\theta}=e^{i(\theta+2\pi)}=e^{i(\theta+2n \pi)}$

for any integer. This is highly problematic. Consider that

$z_1=r e^{i\theta}, \qquad z_2=r e^{i(\theta+2n\pi)}$

represent the same (apparently) complex numbers, but

$\ln z_1=\ln r+i\theta, \qquad \ln z_2=\ln r+i\theta+2n\pi i$

We have the situation in which two different complex numbers, in fact an infinite number of them, have the same}logarithm; the log function is multi-valued. You cannot do calculus with multi-valued functions, what value does one use for the log? You cannot simply take your pick. It is true that for many applications you can select a branch of a multi-valued function, but you must admit all of this injects a certain degree of ambiguity into what should be well-posed problems in calculus with unique solutions.

Riemann solved this very severe dilemma by introducing the notion that $z_1$ and $z_2$ are in fact not the same complex number, at least as far as the log function is concerned. Riemann’s suggestion is to generalize the concept of the domain of the log function, so that $z_1$ and $z_2$ are different points. If the domain is defined correctly, the log function will be single-valued. The correct domain for a complex function is called its Riemann surface, which consists of multiple copies of the complex plane sutured together along cuts that begin and terminate on branch points. The branch points themselves are singularities of the function. The Riemann surface for the log function consists of an infinite number of copies of the complex plane, with a cut extending along the real axis from the origin to negative infinity on each sheet. The sheets are connected with the lower edge of the cut for one sheet sutured to the upper edge of the cut for the sheet “below” it, forming an infinite spiral structure. Two sheets of the surface are illustrated below

In this figure, the lower sheet contains all $z$ for which $-\pi\le \theta < \pi$ , which gets mapped onto what is called the principal branch of the log function

$-i\pi< Im \, \ln z< i\pi, \qquad -\pi \le Arg(z)\le \pi$

Note that along any curve that surrounds the origin, the log function accumulates a total angle of $2\pi$ as the curve is traversed.

the sheet above it contains those points $z$ for which $\pi \le \theta < 3\pi$ , and so forth ad infinitum, in both directions. We can label the sheets $\mathcal{C}_n$ , such that

$(2n-1)i\pi< Im \, \ln z< (2n+1)i\pi, \qquad z \in \mathcal{C}_n$

One should really think of all sheets flattened into the plane, but as K. Knopp says ( Theory of Functions, by K. Knopp, absolutely indispensable) , limitations in human perception prevent us from correctly visualizing the Riemann surface without recourse to an extra dimension.
The most common way to represent a cut, where Riemann sheets are sutured together, is with a wavy line as in the figure above. The precise location of the cut is essentially a coordinate choice, and has no intrinsic meaning.
One can examine a sequence of complex numbers on a path or circle about the origin by increasing $\theta$ . As this angle is increased, you may cross a cut, and in doing so pass from one sheet of the Riemann surface to another.
The square root function is another potentially multi-valued function that will require domain modification

$\sqrt{z}=\sqrt{r \, e^{i\theta}}=\sqrt{r} \, e^{i{\theta\over 2}}$

Notice that

$z_1=r e^{i\theta}, \qquad z_2=r e^{2\pi i +i\theta}$

are apparently the same complex number, but have opposite square roots, however

$z_3=r \, e^{4\pi i +i\theta}$

is such that

$\sqrt{z_1}=\sqrt{z_3}$

, so apparently, the square root function Riemann surface only requires two sheets, passage twice around the origin returns one to the original sheet of the surface, which is illustrated below

Consider traveling around a circle on the Riemann surface. The point $A$ is at $r e^{i{\pi\over 2}}$ on the bottom sheet, $B$ is at $r e^{i\pi}$ also on the bottom sheet, and so is $C$ at $r e^{i{3\pi\over 2}}$ . As we continue on the surface in the direction of increasing $\theta$ , we cross the cut which we situate along the positive real axis from the origin to infinity. This puts us onto the next sheet, ending up at point $D$ at $r \, e^{i{5\pi\over 2}}$ , which we can see in the cut-away view, coloring the two sheets of the surface differently.

If we were to continue onward, traveling another ${3\pi\over 2}$ radians, we would encounter the cut again and pass back onto the lower sheet of the Riemann surface.
Suppose that we were to integrate the square root (reciprocal, which has same Riemann surface) around this circular path, beginning at $B$ and ending at $D$ . Without the essential modifications to the domain of the square root, we would think that we are integrating in a complete circle, after all naively we would say

$B=r \, e^{i{\pi\over 2}}=r \, e^{2\pi i +i{\pi\over 2}}=D$

and then anticipate getting zero for the integral. We would certainly be confused then when the answer did not turn out to be zero

(1) $\begin{eqnarray*}\int_B^D {dz\over \sqrt{z}}=2\sqrt{z}\big{|}_B^D&=&2\sqrt{r}( \sqrt{e^{2\pi i +i{\pi\over 2}}}-\sqrt{e^{i{\pi\over 2}}})\nonumber\\ &=&-2\sqrt{r} \, e^{i{\pi\over 4}}\end{eqnarray*}$

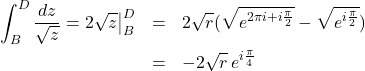
Riemann surfaces for more complicated functions such as

$f(z)={1\over \sqrt{1-z^2}}={1\over \sqrt{(1-z)(1+z)}}$

may have a more subtle level of connectivity. This surface has two cuts and two sheets, the cuts can extend from $z=\pm 1$ to $\pm \infty$ , as in the figure below

The Riemann sheet of the principle branch of this function is shown here.
In order to make sense of these complicated constructions, we use local coordinates

$1-z= r_1 \, e^{i\theta_1}, \qquad 1+z=r_2 \, e^{i\theta_2}$

such that

$\sqrt{(1-z)(1+z)}=\sqrt{r_1 \, r_2} \, e^{i{\theta_1+\theta_2\over 2}}$

The sheet of the principal branch of this function has

$-\pi<Arg (1-z)\le\pi, \qquad -\pi<Arg (1+z)\le\pi$

which results in

$-\pi< Arg(\sqrt{(1-z)(1+z)})\le \pi$

For the angles in these ranges, $\sqrt{(1-z)(1+z)}=\sqrt{r_1 \, r_2} \, e^{i{\theta_1+\theta_2\over 2}}$ is single valued, and we refer to this branch as $F(z)$ . If the angles are outside of this range, we are on the other branch of the function, which is $-F(z)$ .
The disposition of the cuts is irrelevant,in another choice the cuts could extend in the opposite directions, starting on one branch point and terminating on the other.

The Riemann surfaces of inverse trigonometric and inverse hyperbolic functions are all closely related to that of the log function. This can be seen by purely algebraic means. Consider

$\cosh x=y={e^x+e^{-x}\over 2}, \qquad e^{2x}-2y \, e^{x}+1=0$