Physics 7xx: Complex variables-2. Differentiation and integration

Differentiation
We will associate with the point $(x,y)$ in the plane a {\bf complex number} $z=x+iy$ , with $i=\sqrt{-1}=e^{\pi i}$ . We call $\bar{z}=x-iy$ the complex conjugate of $z$ . The transformation $x,y\rightarrow z,\bar{z}$ can be regarded as a simple change of variable. Functions of the form

$f(x,y)=f(z,\bar{z})=f(z)$

in other words, functions of the special combination $z=x+iy$ of $x$ and $y$ , are actually functions of a single variable. However for such functions, the path along which we perform the limit in the derivative process is not unique, for example we can write

$f'(z,\bar{z})=\lim_{\epsilon\rightarrow 0} {f(z+\epsilon)-f(z)\over \epsilon}$

$f'(z,\bar{z})=\lim_{\epsilon\rightarrow 0} {f(z+i\epsilon)-f(z)\over i\epsilon}$

and if these two definitions do not produce the same result, we are in deep trouble since calculus will essentially become dysfunctional.
We will refer to any function whose derivative in the complex plane is unique as being analytic.

${1\over \bar{z}} \qquad \mbox{is not analytic}$

Proof. What a profound difference a sign can make;

(1) $\begin{eqnarray*}{d\over dz}{1\over x-iy}&=&\lim_{\epsilon\rightarrow 0}\big({{1\over x+\epsilon-iy}-{1\over x-iy}\over \epsilon}\big)\nonumber\\ &=&\lim_{\epsilon\rightarrow 0}{1\over \epsilon}\big({1\over \bar{z}(1+{\epsilon\over \bar{z}})}-{1\over \bar{z}}\big)\nonumber\\ &=&\lim_{\epsilon\rightarrow 0}{1\over \epsilon}({-\epsilon\over \bar{z}^2}+\mathcal{O}(\epsilon^2))\nonumber\\ &=&{-1\over \bar{z}^2}\end{eqnarray*}$

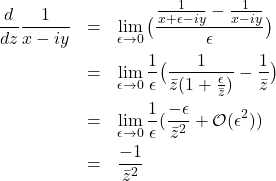
however, if we take the derivative by a different route:

(2) $\begin{eqnarray*}{d\over dz}{1\over x-iy}&=&\lim_{\epsilon\rightarrow 0}\big({{1\over x-i(y+\epsilon)}-{1\over x-iy}\over i\epsilon}\big)\nonumber\\ &=&\lim_{\epsilon\rightarrow 0}{1\over i\epsilon}\big({1\over \bar{z}(1-i{\epsilon\over \bar{z}})}-{1\over \bar{z}}\big)\nonumber\\ &=&\lim_{\epsilon\rightarrow 0}{1\over i\epsilon}({i\epsilon\over \bar{z}^2}+\mathcal{O}(\epsilon^2))\nonumber\\ &=&{1\over \bar{z}^2}\end{eqnarray*}$

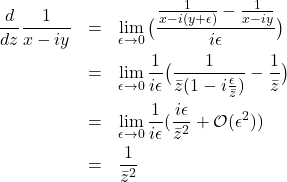
and these two are clearly not the same. Analytic means that the derivative is unique, and independent of the path along which the limit is taken. Notice that ${1\over z}$ is analytic;

(3) $\begin{eqnarray*}{d\over dz}{1\over x+iy}&=&\lim_{\epsilon\rightarrow 0}\big({{1\over x+\epsilon+iy}-{1\over x+iy}\over \epsilon}\big)\nonumber\\ &=&\lim_{\epsilon\rightarrow 0}{1\over \epsilon}\big({1\over \bar{z}(1+{\epsilon\over z})}-{1\over z}\big)=\lim_{\epsilon\rightarrow 0}{1\over \epsilon}{-\epsilon\over z^2+\mathcal{O}(\epsilon^2)}\nonumber\\ &=&{-1\over z^2}\end{eqnarray*}$

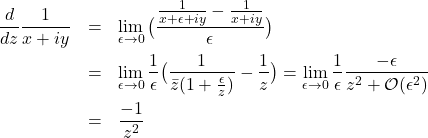
and along a different route;

(4) $\begin{eqnarray*}{d\over dz}{1\over x+iy}&=&\lim_{\epsilon\rightarrow 0}\big({{1\over x+i(y+\epsilon)}-{1\over x+iy}\over i\epsilon}\big)\nonumber\\ &=&\lim_{\epsilon\rightarrow 0}{1\over i\epsilon}\big({1\over z(1+i{\epsilon\over z})}-{1\over z}\big)\nonumber\\ &=&\lim_{\epsilon\rightarrow 0}{1\over i\epsilon}{-i\epsilon\over z^2+\mathcal{O}(\epsilon^2)}={-1\over z^2}\end{eqnarray*}$

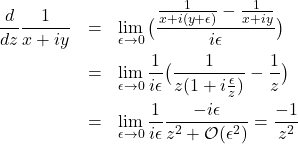
A great deal can be said about the structure of analytic functions, and we will discover that their calculus is extremely simple. Consider a function $f(z, \bar{z})$ , and imagine separating it into two functions, both real, one of them being the coefficient of all occurrances of $i$ . Such a decomposition is called separating the real and imaginary parts of $f$

$f=Re \, f + i \, Im \, f=U(x,y)+iV(x,y)$

Consider

$f(x,y)=(x+3+y+2iy)^2$

separate this into its real and imaginary parts

$f(x,y)=(x+3+y)^2+2\cdot (x+3+y)\cdot 2iy -4y^2$

$Re \, f=(x+3+y)^2-4y^2, \qquad Im \, f=2\cdot (x+3+y)\cdot 2y$

Examples

(5) $\begin{eqnarray*}f(x,y)&=&\sin(x+2iy)=\sin(x) \, \cos(2iy) + \cos(x) \, \sin(2iy)\nonumber\\ &=&\sin(x) \, \cosh(2y) + i\cos(x) \, \sinh(2y)\end{eqnarray*}$

and so

$Re \, f=\sin(x) \, \cosh(2y), \qquad Im \, f=\cos(x) \, \sinh(2y)$

(6) $\begin{eqnarray*}f(x,y)&=&{1\over x+y+3ix}\nonumber\\ &=&{x+y-3ix\over ( x+y+3ix)( x+y-3ix)}\nonumber\\ &=&{x+y\over (x+y)^2+9x^2}-i{3x\over(x+y)^2+9x^2}\end{eqnarray*}$

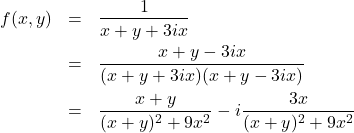
therefore

$Re \, f={x+y\over (x+y)^2+9x^2}, \qquad Im \, f=-{3x\over(x+y)^2+9x^2}$

Which of these functions are analytic, meaning, which possess unique derivatives at points $z=x+iy$ in the plane?
Compute the derivative of $f(x,y)$ first “horizontally”, $z\rightarrow z+\epsilon$ ;

${d\over dz}f(z)=\lim_{\epsilon\rightarrow 0}{U(x+\epsilon,y)+iV(x+\epsilon,y)-U(x,y)+iV(x,y)\over \epsilon}$

${\partial U\over \partial x}+i{\partial V\over \partial x}$

and then “vertically”, $z\rightarrow z+i\epsilon$ ;

${d\over dz}f(z)=\lim_{\epsilon\rightarrow 0}{U(x,y+\epsilon)+iV(x,y+\epsilon)-U(x,y)+iV(x,y)\over i\epsilon}$

${1\over i}{\partial U\over \partial y}+{\partial V\over \partial y}$

If these are supposed to be the same, then

$-{\partial U\over \partial y}={\partial V\over \partial x}, \qquad {\partial U\over \partial x}={\partial V\over \partial y}$

These equations are called the Cauchy-Riemann conditions for analyticity at the point $z=x+iy$ .

Integration
The very simplest of functions of a complex variable are called {\bf entire}, meaning that a power series such as

$f(z)=\sum_{n=0}^\infty a_n z^n$

defines the function at all points in the complex plane. This requires that the power series have an infinite radius of convergence.
Most functions are not this simple, and we have encountered dozens of examples of rational functions that contain singularities; points where they blow up. If we take an arbitrary function $f(z)$ , it could have an entire part $g(z)$ , as well as a partial fraction portion containing all of its singularities. Suppose that the function has a singularity at $z_0$ .
We will refer to the principal part of $f(z)$ for singularity $z_0$ to be

$p^{(0)}_f(z)={a^{(0)}_{-1}\over z-z_0}+{a^{(0)}_{-2}\over (z-z_0)^2}+\cdots +{a^{(0)}_{-N_0}\over (z-z_0)^N}$

and in general a rational function could have many{\bf poles} $z_0, z_1, \cdots, z_\nu$ , and so would have a general structure

$f(z)=\sum_{n=0}^\nu p^{(n)}_f(z)+g(z)$

We will now classify functions in a more detailed way.
If a function possesses a representation in terms of principal parts as illustrated above, with all of its principal parts containing a finite number of terms, we refer to the singularities as poles. If a function has a representation as illustrated above in which a principal part, say for pole $z_\mu$ , has an infinite number of negative power terms, we refer to $z_\mu$ as an essential singularity. A singularity of $f(z)$ at $z=z_0$ is called removable if $f(z)$ is not defined there, but could be. For example the function

$f(z)={z^2-1\over z-1}$

can be defined to be $z+1$ at $z=1$ , thus removing the singularity at $z=1$ .

Any single valued function that has no singularities other than poles at finite magnitude $z$ values is called meromorphic, with no regard to the behavior at infinity. These are the types of functions that we encounter most often in physics.

${1\over \sin z}$ is meromorphic. We could perform a partial fraction decomposition, and discover that the cosecant has only simple poles (poles of order one).

$e^{z}$ is entire, possessing an essential singularity, but it is at infinity.

A function may possess a region of the complex plane upon which it is single valued and differentiable. We say that a function possessing such a region is regular in it. Any function that has a power series valid in the entire complex plane is regular in the entire plane, and is then deemed an entire function.
We will now list and “prove” or at least rationalize some very useful theorems on integration of functions in regions of regularity. We will use the fact that regularity means differentiability, and so the functions involved satisfy the Cauchy-Riemann conditions.
Remember that if

$f(z)=U+iV=U(x,y)+iV(x,y)$

in which $U$ and $V$ are real functions, then for unique derivatives with respect to a single complex variable.
$U$ and $V$ must satisfy

$\frac{\partial U}{\partial x}=\frac{\partial V}{\partial y}, \qquad \frac{\partial U}{\partial y}=-\frac{\partial V}{\partial x}$

and a function $f(z)=U(x,y)+iV(x,y)$ that satisfies this is called an analytic function, and these are the Cauchy-Riemann conditions.
There are two “potentials” that can be constructed from the Cauchy-Riemann conditions. Number one is $\phi$

$U=\frac{\partial \phi}{\partial x},\qquad V=-\frac{\partial \phi}{\partial y}$

which automatically satisfies the second C.R. condition by virtue of ${\partial^2 \phi\over \partial x \, \partial y}={\partial^2 \phi\over \partial y \, \partial x}$ , and satisfies the first C.R. condition if ${\partial^2 \phi\over \partial^2 x}+{\partial^2 \phi\over \partial^2 y}=0$ . Number two is $\psi$

$U=\frac{\partial \psi}{\partial y},\qquad V=\frac{\partial \psi}{\partial x}$

which automatically satisfies the first C.R. condition and satisfies the second if ${\partial^2 \psi\over \partial^2 x}+{\partial^2 \psi\over \partial^2 y}=0$ .
We have established that any analytic function can be constructed from these two “harmonic” potentials

$\nabla^2 \phi=0, \qquad \nabla^2\psi=0$

such that

$U=\frac{\partial \phi}{\partial x},\qquad V=-\frac{\partial \phi}{\partial y}, \qquad U=\frac{\partial \psi}{\partial y},\qquad V=\frac{\partial \psi}{\partial x}$

Now consider any closed path $C$ lying entirely within a simply connect region of regularity, and integrate analytic $f(z)$ along this path. The result can be written in terms of the potentials $\psi$ and $\phi$ ;

$\oint_C f(z) dz=\oint_C (U+iV)(dx+i dy)=\oint_C (U dx-V dy)+i\oint_C( U dy+V dx)$

$=\oint_c d\phi +i\oint_C d\psi$

Therefore both of these integrals should be zero, since a proper real-valued function returns to its original value at a point $(x_0,y_0)$ after we walk along a closed curve starting and ending at this point.

Not so fast. We have already encountered one function that returns to its original value only after twice circling the origin, $f(z)=\sqrt{z}$ , and another that never returns to its original value if the origin is fully circled, namely $f(z)=\ln z$ .

$\oint_C d\ln z=\oint_C {dz\over z}=\oint_C {dx+i \, dy\over x+iy}$

$=\oint_C {x \, dx+y \, dy\over x^2+y^2} +i \oint_C {x \, dy-y \, dx\over x^2+y^2}$

$=\oint_C \half {dr^2\over r^2}+i \oint_C d\theta=0+2\pi i$

and there we have it;
integrals in the complex domain need to be evaluated keeping in mind that terms such as ${dz\over z-a}$ are very special, because of the nature of the Riemann surface of the log function. Technically the imaginary part of ${dz\over z}$ is not an exact differential, because we cannot really construct a closed curve surrounding the singularity on its Riemann surface.

At this point lets appeal to physics and consider a well-understood example, but in the context of complex integration. What does this all have to do with physics anyway? Consider for example a {\bf static} electric field, which is created by a line charge $\lambda$ somewhere in space. We know that the electric field of a line charge is conservative; no work is done in moving a test charge through the field in a closed path. Imagine then that

$f(z)=E_x-iE_y$

for such an electric field $(E_x,E_y)$ , then

$\int_a^b f(z) \, dz=\int_a^b (E_x-i \, E_y)(dx+i \, dy)=\int_a^b(E_x dx +E_y dy)+i\int_a^b (E_x dy -E_y dx)$

The real part of this expression is the work done in moving a unit test charge from $a$ to $b$ through this field!

$W_{a\rightarrow b}=\int_a^b (E_x dx +E_y dy)$

This will be zero if we let $a=b$ and close the path of integration, even if it surrounds the origin, the point through which we let our line charge pass

$E_x={\lambda\over 2\pi\epsilon_0}{x\over x^2+y^2}, \qquad E_y={\lambda\over 2\pi\epsilon_0}{y\over x^2+y^2}$

However in order for $\oint_C f(z) \, dz$ to be zero, we need to have

$i\oint_C (E_x dy -E_y dx)=0$

as well, but this is not true if the path of integration encloses the origin

$i\oint_C (E_x dy -E_y dx)=i\oint_C {\lambda\over 2\pi\epsilon_0}{x \, dy-y \, dx\over x^2+y^2}$

notice that the polar angle $\theta'=\tan^{-1}{y\over x}$ has

$d\theta'=dV={{dy\over x}-{y \, dx\over x^2}\over 1+{y^2\over x^2}}={x \, dy-y \, dx\over x^2+y^2}$

which does not exist at the oigin, and so we must remove the origin from its domain. Then

$i\oint_C (E_x dy -E_y dx)=i\oint_0^{2\pi} {\lambda\over 2\pi\epsilon_0} d\theta'=2\pi i {\lambda\over 2\pi\epsilon_0}\ne 0$

but we can do the integral in a second way and get a different answer

$\oint dV=\oint {dV\over d\theta}d\theta=0$

What went wrong?

Essentially our region in which our path of integration lies is not simply connected; the function $f(z)$ is not defined at the origin, and so we must delete $(0,0)$ from the domain of integration, making it annular, which is not simply connected. If the path of integration was a circle that did not contain the origin (as in the figure below, then this last integral would have been zero and we would have $\oint_C f(z) \, dz=0$ .

$i\oint_C (E_x dy -E_y dx)$

$=i\int_0^{\theta} {\lambda\over 2\pi\epsilon_0} d\theta'+i\int_{\theta}^0 {\lambda\over 2\pi\epsilon_0} d\theta'= 0$

What is the function $f(z)$ ?

$f(z)={\lambda\over 2\pi\epsilon_0}{x\over x^2+y^2}-i{\lambda\over 2\pi\epsilon_0}{y\over x^2+y^2}={\lambda\over 2\pi\epsilon_0} {x-iy\over (x+iy)(x-iy)}={\lambda\over 2\pi\epsilon_0 \, z}$

which is clearly regular in the off-center disk but not in one containing the origin.
Why is this electromagnetic recourse so useful? Consider a region containing an electrostatic field, but no charges. In such a region the electric field satisfies Gausse’s law with no charges, which we will later show means that the voltage $V(x,y)$ satisfies

${\partial^2\over \partial x^2}V(x,y)+{\partial^2\over \partial y^2}V(x,y)=0$

a simple variable change $z=x+iy$ , $\bar{z}=x-iy$ gives us

$4{\partial^2 \over \partial z \, \partial \bar{z}}V(z, \bar{z})=0$

which is true if

$V(z, \bar{z})=V(z)$

and so the voltage is a regular, analytic function in such a region!

An immediate corollary of our theorem is
Theorem.
For any simply connected domain of regularity;

$\int_{C_1} f(z) \, dz=\int_{C_2} f(z) \, dz$

where $C_1$ and $C_2$ are two curves both beginning on $a$ and ending on $b$ .
This one is simple, take the two curves and combine them to make a closed curve $C$

$\oint_C f(z) \, dz=0=\int_a^b f(z) \, dz +\int_b^a f(z) \, dz$

in which we go from $a$ to $b$ along $C_1$ in the first integral, but the wrong way on $C_2$ on the second, resulting in

$\int_{C_1} f(z) \, dz=\int_{C_2} f(z) \, dz$

The most important regions in which to embed integration paths for our purposes will be annular regions surrounding singularies
made by adjoining two simply connected regions of regularity for a function $f(z)$ .
Such a region has an inner bounding curve $C_1$ , an outer bounding curve $C_2$ , and between them a regular function could have a convergent partial fraction representation called a Laurent series

$f(z)=\sum_{n=-\infty}^\infty a_n (z-z_0)^n$

however this region is not simply connected, and that is the source of all of the power.

Theorem. Consider any region of regularity for $f(z)$ , simply connected or not. Let $C_1$ and $C_2$ be any closed curves lying within that region, both surrounding the inner bounding curve of the domain of regularity.

$\oint_{C_1} f(z) \, dz=\oint_{C_2} f(z) \, dz$

Why is this so important? It says that when doing a line integral in an annular region, the path of integration is immaterial, simply choose the one that is easiest to work with.}} All that matters in the end is the fact that the paths enclose poles of $f(z)$ . The proof is simple. Consider the curve $C_1$ to be the innermost, drawn here within the shaded region of regularity, and $C_2$ to be the outer.

Connect them with pairs of bridges, dividing the region between them into two simply connected domains of regularity $R$ and $S$ . Then denoting the boundaries of $R$ and $S$ by $\partial R$ and $\partial S$ respectively

$\oint_{\partial R} f(z) \, dz=0=\oint_{\partial S} f(z) \, dz$

However the integrations over the pairs of bridges, being arbitrarily close together, cancel, and so

$\oint_{\partial R} f(z) \, dz+\oint_{\partial S} f(z) \, dz=0=\oint_{-C_1} f(z) \, dz=0+\oint_{C_2} f(z) \, dz=0$

in which we use $-C_1$ to indicate that we are integrating around $C_1$ in the negative sense, and so

$-\oint_{-C_1} f(z) \, dz=\oint_{C_1} f(z) \, dz=\oint_{C_2} f(z) \, dz$

as we wanted to show.

Our final two theorems are what makes complex variables so powerful in integration, and in solving electromagnetism applications.
Theorem. A regular function on a region of regularity $R$ has its interior values determined entirely by the values of $f(z)$ on the boundary of the region of regularity

$f(z)={1\over 2\pi i} \oint_{\partial R} {f(z') \, dz'\over z'-z}$

in electromagnetism, this is called the Mean Value theorem, and is used to compute voltages in charge free volumes numerically by relaxation techniques.
We will “prove” this theorem in a way that you will emulate in nearly all computational situations. First let’s write

${1\over 2\pi i} \oint_{\partial R} {f(z') \, dz'\over z'-z}={1\over 2\pi i} \oint_{\partial R} {f(z) \, dz'\over z'-z}+{1\over 2\pi i} \oint_{\partial R} {f(z') -f(z)\, dz'\over z'-z}$

and invoke the previous theorem; the path of integration is immaterial, deform the contour to a simple one; a circle $C$ of very small radius around $z$

${1\over 2\pi i} \oint_{\partial R} {f(z') \, dz'\over z'-z}={1\over 2\pi i} \oint_{C} {f(z') \, dz'\over z'-z}$

$={1\over 2\pi i} \oint_{C} {f(z) \, dz'\over z'-z}+{1\over 2\pi i} \oint_{C} {f(z') -f(z)\, dz'\over z'-z}$

for which

$z'=z+r e^{i\theta}$

then

${1\over 2\pi i} \oint_{\partial R} {f(z') \, dz'\over z'-z}={f(z)\over 2\pi i}\int_0^{2\pi} {ir e^{i\theta} \, d\theta\over r e^{i\theta}}+{1\over 2\pi i} \oint_{C} {f(z') -f(z)\, dz'\over z'-z}$

$=f(z)+{1\over 2\pi i} \oint_{C} {f(z') -f(z)\, dz'\over z'-z}$

and use the fact that our function, being regular in this domain, possesses a valid power series around $z$ ;

$f(z')=f(z)+(z'-z)f'(z)+{1\over 2!}(z'-z)^2 f''(z)+\cdots$

$=f(z)+r e^{i\theta} f'(z)+{r^2\over 2!} e^{2i\theta} f''(z)+\cdots$

Put these into our last integral, and shrink $r$ down to nothing, all of these integrals become zero

${1\over 2\pi i} \oint_{C} {f(z') -f(z)\, dz'\over z'-z}$

$={1\over 2\pi i}\int_0^{2\pi}{ ir e^{i\theta} \, d\theta\over r^{i\theta}}\big(r e^{i\theta} f'(z)+{r^2\over 2!} e^{2i\theta} f''(z)+\cdots\big)\rightarrow 0$

since each one contains a positive power of $r$ .

Our final theorem is the most powerful of all, and enables us to not only do the most fantastic feats of integration, but can also be used to extract information of all types from functions, including their periodicity properties, and asymptotic behaviors.
Cauchy’s Theorem.
Let the curve $C$ lie within an annular region of regularity for some function $f(z)$ . Then

$\oint_C f(z) \, dz=2\pi i \sum_n a^{(n)}_{-1}$

in which $a^{(n)}$ is the coefficient of the term ${1\over z-z_n}$ in the principal part of $f(z)$ for pole $z_n$ . These are called the {\bf residues} of the function, and this is often referred to as the residue theorem.

The proof is almost trivial; Since the shape of the contour is irrelevant as long as it encloses the pole, let $C$ be a circle of radius $r$ around the pole of $f(z)$ at $z_0$ , then $z=z_0+r e^{i\theta}$ , $dz=ir \, e^{i\theta} \, d\theta$ and the function $f(z)$ possesses a Laurent series in the annular region surrounding the pole, the region in which $C$ is drawn.

$\oint_C f(z) \, dz=\int_0^{2\pi} ir e^{i\theta} \, (\sum_{n=-\infty}^\infty a_{n} \, r^n e^{in\theta}) \, d\theta$

$\mbox{but}\quad \int_0^{2\pi} e^{in\theta} \, d\theta=0, \qquad n\ne 0$

and is $2\pi$ if $n=0$ . Only the residue term survives the integration

$\oint_C f(z) \, dz=2\pi i a_{-1}$

Why is this so powerful? It reduces the difficult problem of integration to simply finding certain coefficients of a functions Laurent series. To evaluate integrals, we simple compute residues at poles $z_0$

$res_{z_0}=\lim_{z\rightarrow z_0} \, (z-z_0) f(z)$

Home 2.0

Physics 7xx: Complex variables-2. Differentiation and integration

Related Posts

Physics 7xx: Complex variables-2. Differentiation and integration

Published by Jeff on December 2, 2021December 2, 2021

Related Posts

Physics 7xx: Evaluating action integrals ala’ Sommerfeld

Protected: Physics 711: PS-6 solutions

Protected: Physics 711: Lecture 38