To evaluate
![]()
where ![]() we pass to the complex
we pass to the complex ![]() plane and construct an annular region around the cut that allows us to construct a two-sheeted Riemann surface domain on which the integrand is a single-valued function. I think that this was introduced by Sommerfeld. We will use the augmented complex plane (Riemann sphere)
plane and construct an annular region around the cut that allows us to construct a two-sheeted Riemann surface domain on which the integrand is a single-valued function. I think that this was introduced by Sommerfeld. We will use the augmented complex plane (Riemann sphere) ![]() by adjoining to the plane the point at infinity, this can be visualized as the sphere that is mapped to the plane tangent to the sphere at the south pole by stereographic mapping using rays from the north pole through points on the sphere onto points on the plane.
by adjoining to the plane the point at infinity, this can be visualized as the sphere that is mapped to the plane tangent to the sphere at the south pole by stereographic mapping using rays from the north pole through points on the sphere onto points on the plane.

Note the direction of the contour, the “positive sense”. I usually use only the ability to deform the contour, plus “brute force integration” of parameterizing each segment of the path, plus taking care to evaluate all phases on the same branch, for example ![]() .\\
.\\
The cut between the turning points can be disposed in any way that we which on the plane/sphere as long as it connects the turning points. Note then that the rest of the Riemann sphere forms an annular region. There is singularity at infinity. Exploit the invariance of the integral ![]()
![]()
under “rubber-band” deformations of the contour ![]() and the cut itself, stretching both around the Riemann sphere as in the sequence of figures.
and the cut itself, stretching both around the Riemann sphere as in the sequence of figures.

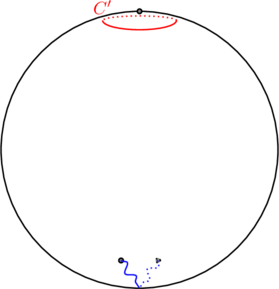
The new contour ![]() encircles the point at infinity, on
encircles the point at infinity, on ![]() we have
we have ![]() and we first integrate over
and we first integrate over ![]() then let
then let ![]() . We must expand the integrand in a series that converges for large
. We must expand the integrand in a series that converges for large ![]() ;
;
![]()
Not happy with this? Try rubber-banding the cut and contour as shown below…

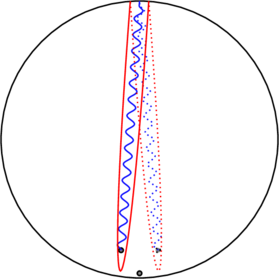

The result of which is equivalent to having simply selected the disposition of the cut to be as shown here, closing the contour at infinity (not shown) to form a loop contractible to a circle around the origin;
but just be be sure, let’s evaluate all eight parts of the integral (parts ![]() not shown)
not shown)
(1) 
Hopefully you can see that (1) and (7) cancel, (3) and (5) cancel, (4) and (8) are both zero, and (2) and (6) add up to what we obtained using the first deformation. Phew!