Physics 7xx: Ehrenfest’s theorem

What is the time dependence of an expectation value? In the Schrodinger picture

(1) $\begin{eqnarray*}\frac{d}{dt}\langle \hat{A}\rangle&=&\frac{d}{dt}\langle\psi(t)|\hat{A}(t)|\psi(t)\rangle \nonumber\\ &=&\frac{1}{i \hbar}(\langle\psi|[\hat{A},\hat{H}]|\psi\rangle+\langle\psi|\frac{d\hat{A}}{dt}|\psi\rangle \end{eqnarray*}$

using $i\hbar {d\over dt}|\psi(t)\rangle=\hat{H}|\psi(t)\rangle$ .
This formula sees a lot of applications in atomic physics, it is handy for constructing sum rules.

What if $\psi(x,t)$ represents a stationary state? Then $\psi(x,t)=\psi(x,0) e^{-iEt/\hbar}$ and

$\langle\psi|[\hat{A},\hat{H}]|\psi\rangle=\langle |\hat{A}\hat{H}-\hat{H}\hat{A}|\psi\rangle=\langle |\hat{A}E-E\hat{A}|\psi\rangle=0$

by hermiticity of $\hat{H}$ : $\hat{H}|\psi\rangle=E|\psi\rangle$ , $\langle \psi|\hat{H}=\langle \psi| E$ for stationary states.

Note that in general ${d\over dt}\langle\hat{A}\rangle\ne \langle{d\hat{A}\over dt}\rangle$ , you must have $[\hat{A},\hat{H}]=0$ for this to be true.
We will now use the fact that the Hamiltonian is the time evolution operator to prove Ehrenfest’s Theorem. Classically

(2) $\begin{eqnarray*} {dA\over dt}&=&{\partial A\over \partial q} {dq\over dt}+{\partial A\over \partial p} {dp\over dt}+{\partial A\over \partial t}=0\nonumber\\ &=&{\partial A\over \partial q}{\partial H\over \partial p}-{\partial A\over \partial p} {\partial H\over \partial q}+{\partial A\over \partial t}\nonumber\\ &=&\{A,H\}_{PB}+{\partial Q\over \partial t}\end{eqnarray*}$

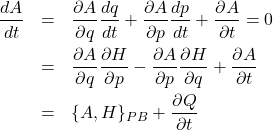
Perform canonical quantization

${d\hat{A}\over dt}={1\over i\hbar}[\hat{A}, \hat{H}]+ {\partial\hat{A}\over \partial t}$

and take expectation values

$\langle {d\hat{A}\over dt}\rangle={1\over i\hbar}\langle[\hat{A}, \hat{H}]\rangle+\langle {\partial\hat{A}\over \partial t}\rangle$

let $\hat{A}=\hat{x}$ , and use the fact that $\hat{H}=\hat{H}(\hat{x}, \hat{p})$ and the derivation rule for commutators

$}\langle {d\hat{x}\over dt}\rangle={1\over i\hbar}\langle[\hat{x}, \hat{H}]\rangle={1\over i\hbar}\langle[\hat{x}, \hat{p}] {\partial\hat{H}\over \partial \hat{p}}\rangle=\langle{\partial\hat{H}\over \partial\hat{p}}\rangle$

Similarly let $\hat{A}(\hat{x}, \hat{p}, t)=\hat{p}$ , then

$\langle {d\hat{p}\over dt}\rangle={1\over i\hbar}\langle[\hat{p}, \hat{H}]\rangle=-\langle{\partial\hat{H}\over \partial\hat{x}}\rangle$

and the proof is complete; expectation values of the position and momentum operators obey the classical equations of motion.

In classical physics conserved quantities have zero time derivative. If dynamical variable $Q=Q(p,q,t)$ is conserved

${dQ\over dt}=0=\{Q,H\}_{PB}$

Quantum mechanically we see a direct translation through the Correspondence Principle; operator $\hat{Q}$ represents a conserved quantity if

$[\hat{Q},H(t')]=0, \, \, \forall \, t'$

If this is true, then

$[\hat{Q}, \mathcal{T} \, e^{-{i\over \hbar}\int_0^t \hat{H}(t') \, dt'}]=0$

by use of our definition of time ordering, and this implies that if

$\hat{Q} \Psi_\xi(0) =\xi \, \Psi_\xi(0)$

then

(3) $\begin{eqnarray*} \hat{Q} \Psi_\xi(t)&=&\hat{Q}\Big((\mathcal{T} \, e^{-{i\over \hbar}\int_0^t \hat{H}(t') \, dt'} \Psi_\xi(0)\Big)\nonumber\\ &=&\mathcal{T} \, e^{-{i\over \hbar}\int_0^t \hat{H}(t') \, dt'}(\hat{Q}\Psi_\xi(0))\nonumber\\ &=&\mathcal{T} \, e^{-{i\over \hbar}\int_0^t \hat{H}(t') \, dt'} (\xi \, \Psi_\xi(0))\nonumber\\ &=&\xi \, \Psi_\xi(t)\end{eqnarray*}$

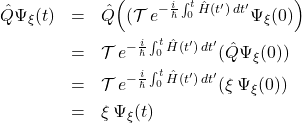
and so the same wavefunction is an eigenstate of $\hat{Q}$ with the same eigenvalue at a later time; that eigenvalue was the value of a conserved quantity.

In the Heisenberg picture the operators carry the time dependence, the wavefunctions do not. A useful observation can be made about how the Heisenberg picture operator acts on wavefunctions.

$i\hbar \frac{d}{dt}\psi=\hat{H}\psi$

can be formally integrated to

$\psi(x,t)=e^{\frac{-i}{\hbar} \hat{H}} \psi(x,0)$

if the Hamiltonian is not explicitly $t$ -dependent, as is the usual case if we are not interacting with external fields. In the Heisenberg picture

$\hat{A}_H(t)=e^{\frac{i}{\hbar}\hat{H}} \hat{A}_S e^{-\frac{i}{\hbar}\hat{H}}$

Suppose that the wavefunction above is an eigenstate of $\hat{A}_S$ of eigenvalue $\lambda_a$

$\hat{A}_S \psi(x,0)=\lambda_a\psi(x,0)$

this can be written as

$\hat{A}_S e^{\frac{i}{\hbar} \hat{H}} \psi(x,t)=\lambda_a \, e^{\frac{i}{\hbar}\hat{H}} \psi(x,t)$

or, since $\lambda_a$ is just a number

$e^{-\frac{i}{\hbar}\hat{H}} \, \hat{A}_S \, e^{\frac{i}{\hbar}\hat{H}}\psi(x,t)=\lambda_a \, \psi(x,t)=\hat{A}_H (-t) \, \psi(x,t)$

The eigenvalue of the Heisenberg picture of the operator at time $-t$ is the eigenvalue of the Schrodinger picture of the operator at time $t=0$ . This can be used to compute the green function for any system in a very easy way.

The free particle. Recall that the green function satisfies

$G(x-x_0,t=0)=\delta(x-x_0)$

and so $G(x-x_0,0)$ is an eigenfunction of the position operator $\hat{x}=x$ at time $t=0$ with eigenvalue $x_0$ . From the above analysis $G(x-x_0,t)$ is an eigenfunction of the Heisenberg version of the same operator evaluated at time $-t$

$\hat{x}_H (-t) \, G(x-x_0,t)=x_0 \, G(x-x_0,t)$

This operator can easily be found from $\hat{H}$

(4) $\begin{eqnarray*}i \hbar \frac{d}{dt}x_H&=&[x_H,\frac{\hat{p}_H^2}{2m}]=-\frac{i \hbar}{m} \, \hat{p}_H \nonumber\\ \mbox{and similarly}\quad i\hbar \frac{d}{dt}\hat{p}_H&=&[\hat{p}_H,\frac{p_H^2}{2m}]=0 \nonumber\\ \mbox{which can be integrated to give}\quad \hat{x}_H(t)&=&\hat{x}_H(0)-\frac{i\hbar t}{m}\frac{d}{dx} \end{eqnarray*}$

because the second of these formulas implies that

$\hat{p}_H(t)=\hat{p}_H (0)=\hat{p}_S=-i\hbar \frac{d}{dx}\quad \mbox{since}\quad [\hat{H}, \hat{p}_S]=0=[e^{\pm i\hat{H}t/\hbar},\hat{p}_S]$

therefore we have a simple first order equation for the Green function

$\Big(x+\frac{i\hbar t}{m}\frac{d}{dx}\Big)G(x-x_0,t)=x_0 \, G(x-x_0,t)$

$G(x-x_0,t)=G_0 \, e^{\frac{-m(x-x_0)^2}{2it \hbar}}$

Home 2.0

Physics 7xx: Ehrenfest’s theorem

Related Posts

Physics 7xx: Ehrenfest’s theorem

Published by Jeff on November 26, 2021November 26, 2021

Related Posts

Physics 7XX: The virial theorem

Protected: GRE-prep: The wavefunction

Protected: Universal relations in thermodynamics