In order to see the “optical” nature of the Hamilton-Jacobi equation, contemplate the physics of waves propagating through a spatially non-isotropic media. Ordinary waves in an isotropic media would obey the standard wave equation
![]()
in which the index of refraction is constant. The solution is, for example
![]()
Wavefronts (surfaces upon which ![]() has the same phase everywhere) are planar and always remain so. Now consider the case in which
has the same phase everywhere) are planar and always remain so. Now consider the case in which ![]() , (spatial anisotropy) and look for solutions of the form
, (spatial anisotropy) and look for solutions of the form
![]()
The function ![]() gives the loci of wavefront, surfaces of constant phase
gives the loci of wavefront, surfaces of constant phase ![]()
![]()
Substitute this into the Helmholtz equation
![]()
Let’s construct an optical model of mechanics starting here, by finding a regime in which the wave equation above becomes more or less the H-J equation. Compute the derivatives on the left side from our explicit expression for ![]() in the optical formulation
in the optical formulation
![]()
For very short ![]() or large
or large ![]() we can neglect the left-most term to obtain
we can neglect the left-most term to obtain
![]()
which we compare to the Hamilton-Jacobi equation
![]()
It appears that classical mechanics is the short wavelength limit of a geometrical optical theory in which the index of refraction for waves is a function of the potential energy
![]()
in which ![]() is some proportionality constant, which can depend only on constants of the motion.
is some proportionality constant, which can depend only on constants of the motion.
Notice that the characteristic function ![]() looks a lot like the phase of the wave
looks a lot like the phase of the wave
![]()
Our new wave mechanics can simultaneously reduce to classical physics ala’ the Hamilton-Jacobi formalism {\bf and} have as consequences both the Planck and De’ Broglie hypotheses by an appropriate choice of ![]() . Substitute
. Substitute ![]() into our proposed waveform to obtain
into our proposed waveform to obtain
![]()
Then if ![]() , we can write
, we can write
![]()
and since ![]() has units of action, we see that
has units of action, we see that ![]() must have units of reciprocal action. Invent a new constant
must have units of reciprocal action. Invent a new constant ![]() up to this point unspecified, with units of action so that
up to this point unspecified, with units of action so that
![]()
Our waveform that ultimately (in the short wavelength limit) returns us to the Hamilton-Jacobi version of classical mechanics is
![]()
Now for a free particle ![]() and so
and so ![]() , which means that our new formalism describes a free particle if
, which means that our new formalism describes a free particle if
![]()
This requirement simultaneously forces
![]()
which are the Planck and De Broglie hypotheses respectively if the constant ![]() is chosen to be Planck’s constant over two pi:
is chosen to be Planck’s constant over two pi: ![]() !
!
The requirement that the new theory reproduces the correct expression for a free particle waveform pins down the constant ![]() and finally determines the “index of refraction” which you discovered in your solution to scattering problems
and finally determines the “index of refraction” which you discovered in your solution to scattering problems
![]()
Since Hamilton-Jacobi theory and this realization that it is the short wavelength limit of an optical theory is several hundred years old, it could be claimed that it was a short hop to a quantum theory, that could have been made 150 years ago. However at that time there was no evidence that a wave optics mechanical theory was correct since no experiments had revealed that matter possessed any wave-like properties, therefore no incentive to push this idea to the stage where the Planck and De’Broglie hypotheses emerge.
Let’s state our optical model for the record:
The mechanical motion of a classical body in a potential is such that it is described by waves whose wavefronts are perpendicular to rays which are the classical trajectories gotten from the Hamilton equations of motion. In addition the theory provides us with a lowest order semi-classical approximation for the wave-function
![]()
which is the first stage of the WKB approximation. If we insert this into the Schr\”odinger wave equation
![]()
we obtain the result
![]()
Which reduces nicely to the Hamilton-Jacobi equation provided that
![]() , so that the leading term is by far the dominant contribution, ie
, so that the leading term is by far the dominant contribution, ie
![]()
alternatively in the limit where ![]() .
.
We regard quantum effects as those proportional to ![]() and these vanish in the limit in which terms of order
and these vanish in the limit in which terms of order ![]() can be neglected.
can be neglected.
The Schrodinger equation is a reformulation of particle mechanics. Consistent with the results of experiments that indicate that very small matter objects behave like waves, Schrodinger wave mechanics describes such objects as being waves that obey a wave equation that in the short wavelength limit reduces to the Hamilton-Jacobi equation. We have not derived Schrodinger from Hamilton-Jacobi, but have instead derived the Hamilton-Jacobi formulation of classical mechanics from the Schrodinger equation as a short wavelength limit, or the limit in which the wavelength is very small compared to the length scales of the mechanical problem.
We can obtain corrections to the classical form if we assume a form for the wavefunction (trying to treat the quantum problem using purely classical formalisms)
![]()
and expand in powers of ![]()
![]()
and insert into the Schr\”odinger equation
![]()
![]()
![]()
This results in
![]()
so that
![]()
We expect that this form breaks down (since ![]() ) at a classical turning point, because near
) at a classical turning point, because near ![]() ,
, ![]() we can expand in a series
we can expand in a series
![]()
Rewrite the condition
![]()
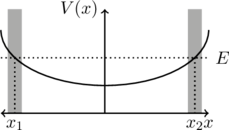
This condition is violated at our turning points ![]() since
since ![]() , so the formulas gotten by the WKB expansion are only valid in regions not to close to the classical turning points. There is a “buffer zone”
, so the formulas gotten by the WKB expansion are only valid in regions not to close to the classical turning points. There is a “buffer zone” ![]() and
and ![]() around each turning point
around each turning point ![]() in which the WKB wavefunctions do not satisfy the validity condition.
in which the WKB wavefunctions do not satisfy the validity condition.
The validity constraint can be rewritten using ![]() expanded near a turning point
expanded near a turning point
![]()
as
![]()
so the WKB wavefunctions are valid for ![]() that obey
that obey
![]()
for turning points ![]() . In the region with
. In the region with ![]() for which this is true, ie
for which this is true, ie ![]() our solution gotten above is just fine
our solution gotten above is just fine
![]()
in which ![]() are constants.
are constants.
In the classically forbidden region ![]() ,
, ![]() also have valid solutions that decay
also have valid solutions that decay
![]()
with ![]()
In the interpolating region ![]() we should not ignore the slope of
we should not ignore the slope of ![]() , but we can say that if the region is very narrow that
, but we can say that if the region is very narrow that ![]() . In the buffer zone then
. In the buffer zone then
![]()
![]()
![]()
![]()
![]()

Both ![]() and
and ![]() are oscillatory for
are oscillatory for ![]() and exponential for
and exponential for ![]() . Since we have forms like
. Since we have forms like ![]() and
and ![]() , as
, as ![]() if
if ![]() then
then ![]() and we can use the exponential asymptotic form. If
and we can use the exponential asymptotic form. If ![]() then
then ![]() and we can use the oscillatory asymptotic form (ie once we depart from
and we can use the oscillatory asymptotic form (ie once we depart from ![]() we have
we have ![]() ). We can rewrite
). We can rewrite ![]() in this region as
in this region as
![]()
Long story short, the WKB wavefunctions, valid outside of the buffer zone, must agree with the asymptotic forms of the exact solution written in terms of Airy functions.
We can show that a solution to the Schrodinger equation that vanishes at ![]() can be written three ways
can be written three ways
![Rendered by QuickLaTeX.com \[\psi(x)=\left\{\begin{array}{ll} {1\over 2\sqrt{q(x)}}e^{-\int_x^{x_1} q(x') \, dx'/\hbar}, & x\sim-\infty\\ & \\ {\sqrt{\pi}\over (2mF\hbar)^{1/6}}\, Ai( ({2mF\over \hbar^2})^{1/3}(x_1-x)), & x\sim x_1\\ & \\ {1\over \sqrt{p(x)}}\cos(\int_x^{x_1} p(x') dx'/\hbar -{\pi\over 4}), & x_1<x< x_2 \end{array}\right.\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-e7db15e292e116dd2b73df142446b24c_l3.png)
The first and last forms are our WKB solutions. The middle one is the exact solution in the buffer zone. We will need the asymptotic forms in Lebedev 5.17.8, 5.17.11
![Rendered by QuickLaTeX.com \[Ai(x)=\left\{\begin{array}{ll}{1\over 2\sqrt{\pi} \, x^{1/4}}e^{-{2\over 3}x^{3/2}} & x\rightarrow \infty\\ {1\over \sqrt{\pi} \, (-x)^{1/4}}\cos({2\over 3}(-x)^{3/2}-{\pi\over 4}) & x\rightarrow -\infty\end{array}\right.\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-325a4f76e15d6ecb74636a2f18b917e3_l3.png)
Here is our proof: within the buffer zone the WKB solution is
\
(1) 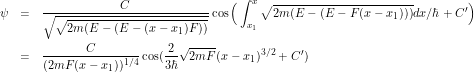
This agrees with the Airy function form if ![]() and
and ![]()
![]()
and of course it all works similarly at the other turning point (we picked ![]() so I only have to do this once)
so I only have to do this once)
![Rendered by QuickLaTeX.com \[\psi(x)=\left\{\begin{array}{ll} {1\over 2\sqrt{q(x)}}e^{-\int_{x_2}^{x} q(x') \, dx'/\hbar}, & x\sim \infty\\ & \\ {\sqrt{\pi}\over (2mF\hbar)^{1/6}}\, Ai( ({2mF\over \hbar^2})^{1/3}(x-x_2)), & x\sim x_2\\ & \\ {1\over \sqrt{p(x)}}\cos(-\int_x^{x_2} p(x') dx'/\hbar +{\pi\over 4}), & x_1<x< x_2 \end{array}\right.\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-ea5f58c2c7d748b5256213b4c89553e8_l3.png)
Finally we compare the exponents of the two formulas for ![]() between
between ![]() .
.
![]()
If
![]()
then the two forms give the same ![]() , so we arrive at a quantization condition reminiscent of Bohr-Sommerfeld, with turning-point corrections
, so we arrive at a quantization condition reminiscent of Bohr-Sommerfeld, with turning-point corrections
![]()
where ![]() is the number of classical turning points (the Maslov index).
is the number of classical turning points (the Maslov index).
What about a hard reflection, such as at a “wall” beyond which the potential goes to infinity? Since ![]() very strongly as
very strongly as ![]() and the slope
and the slope ![]() of such a potential wall is infinity, a hard wall at
of such a potential wall is infinity, a hard wall at ![]() would have
would have
(2) 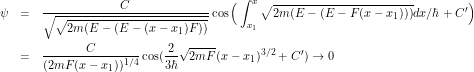
as ![]() , and
, and
![]()
![]()
The EKB energy formula then looks like
![]()
where ![]() is the number of hard bounces on the orbit.
is the number of hard bounces on the orbit.
For example, a particle in a box has two bounces and no true classical turning points, so ![]() and
and ![]() ,
,
![]()
A particle bouncing in a gravitational field of acceleration ![]() has one bounce and one classical turning point at
has one bounce and one classical turning point at ![]()
![]()