Physics 7xx: The hydrogen atom according to Dirac

Our latest 711 homework assignment has a remarkable problem on it: using Bohr’s quantization of the action, work out the spectrum of an electron in a hydrogenic atom treating the problem relativistically, in other words let

$H=\sqrt{m^2c^4+c^2\bm{p}^2}-{k\over r}, \quad k={Ze^2\over 4\pi\epsilon_0}$

This calculation was done by Sommerfeld, and results in a spectrum that in spectacularly good agreement with that gotten from the full Dirac equation. Students (hope you are one) are asked to compare, so let’s look at the Dirac result.

We start with the free Dirac equation

$\left(\begin{array}{cccc}m&0&P_z&-iP_y+P_x\\0&m&iP_y+P_x&-P_z\\P_z&-iP_y+P_x&-m&0\\iP_y+P_x&-P_z&0&-m\end{array}\right)\left(\begin{array}{c}\psi_1\\\psi_2\\\psi_3\\\psi_4\end{array}\right)=i\frac{\partial}{\partial t}\left(\begin{array}{c}\psi_1\\\psi_2\\\psi_3\\\psi_4\end{array}\right)$

and add the potential, and rewrite.
First of all we write out the Dirac equation by splitting the $4$ -spinor into two $2$ -spinors

$\left(\begin{array}{cc}m-E-\frac{k}{r}&\bm{\sigma}\cdot \mathbf{p}\\ \bm{\sigma}\cdot\mathbf{p}&-m-E-\frac{k}{r}\end{array}\right)\left(\begin{array}{c}\phi\\\chi\end{array}\right)=0$

and since we know that this operator H commutes with total angular momentum $\mathbf{J}$ decompose the spinors into radial functions times eigenstates of $J^2$ and $J_z$

$\left(\begin{array}{c}\phi\\\chi\end{array}\right)=\left(\begin{array}{c}A(r)\chi_{ljm}\\B(r)\chi_{ljm}\end{array}\right)$

where for example

$\chi_{ljm}=\left(\begin{array}{c}\sqrt{l+\frac{1}{2}+m}Y_{l,m-\frac{1}{2}}\\-\sqrt{l+\frac{1}{2}-m}Y_{l,m+\frac{1}{2}}\end{array}\right)$

We now employ a trick to speed up the computation. Notice that

$\bm{\sigma}\cdot\hat{r}=\frac{1}{r}\left(\begin{array}{cc}z&x-iy\\x+iy&-z\end{array}\right)$

and that

$(\bm{\sigma}\cdot\hat{r})^2=1$

Incorporate this:

$\bm{\sigma}\cdot\mathbf{p} \, A(r)=[\bm{\sigma}\cdot\hat{r}]^2\bm{\sigma}\cdot\mathbf{p} \, A(r)$

and obtain

$\bm{\sigma}\cdot\hat{r}\bm{\sigma}\cdot\mathbf{p}=\frac{1}{r}(\mathbf{r}\cdot\mathbf{p}+i\bm{\sigma}\cdot\mathbf{L})=\frac{1}{r}\left(\begin{array}{cc}-ir\frac{d}{dr}+iL_z&L_{-}\\L_{+}&-ir\frac{d}{dr}-iL_z\end{array}\right)$

and application of the angular momentum operators gives us

$\left(\begin{array}{cc}L_z&L_{-}\\L_{+}&-L_z\end{array}\right)\left(\begin{array}{c}\sqrt{l+\frac{1}{2}+m}Y_{l,m-\frac{1}{2}}\\-\sqrt{l+\frac{1}{2}-m}Y_{l,m+\frac{1}{2}}\end{array}\right)$

$=(j-\frac{1}{2})\left(\begin{array}{c}\sqrt{l+\frac{1}{2}+m}Y_{l,m-\frac{1}{2}}\\-\sqrt{l+\frac{1}{2}-m}Y_{l,m+\frac{1}{2}}\end{array}\right)$

OK then, we put all of this together

$\bm{\sigma}\cdot\mathbf{p}A(r)\chi_{ljm}=\frac{-i\bm{\sigma}\cdot\hat{r}}{r}(r\frac{d}{dr}-(j-\frac{1}{2}))A(r)\chi_{ljm}$

and

$\bm{\sigma}\cdot\mathbf{p}(\bm{\sigma}\cdot\hat{r}A(r)\chi_{ljm}=\frac{-i}{r}(r\frac{d}{dr}+j+\frac{3}{2})A(r)\chi_{ljm}$

We now rename our spinor components to get rid of this annoying $\bm{\sigma}\cdot\hat{r}$

$A(r)=\frac{ig(r)}{r}, \qquad B(r)=\frac{f(r)\bm{\sigma}\cdot\hat{r}}{r}$

and we arrive at the radial equations

$(E-m+\frac{Ze^2}{r})g=-(\frac{d}{dr}+\frac{j+\frac{1}{2}}{r})f$

$(E+m+\frac{Ze^2}{r})f=(\frac{d}{dr}+\frac{j-\frac{1}{2}}{r})g$

These can be solved by conventional means, and by eliminating $f$ or $g$ we arrive at a Hypergeometric equation.

We perform the following wavefunction redefinition

$f=e^{-\sqrt{m^2-E^2}r}\sqrt{m-E}(F_1(r)-F_2(r)$

$g=e^{-\sqrt{m^2-E^2}r}\sqrt{m+E}(F_1(r)+F_2(r)$

and define

$\sigma=\sqrt{m^2-E^2}$

to arrive at the equations

$(r\frac{d}{dr}-\frac{Ze^2E}{\sigma})F_2=(\frac{Ze^2m}{\sigma}+j+\frac{1}{2})F_1$

$(r\frac{d}{dr}+\frac{Ze^2E}{\sigma}-2\sigma r)F_1=(-\frac{Ze^2m}{\sigma}+j+\frac{1}{2})F_2$

eliminate $F_1$

$(r^2\frac{d^2}{dr^2}+r\frac{d}{dr}-2\sigma r^2\frac{d}{dr}-2Ze^2Er-(\gamma)^2)F_2=0$

where

$\gamma^2=(j+\frac{1}{2})^2-z^2e^4$

Notice that the exponential function enforces the boundary condition that the wavefunction vanish in the classically forbidden region $r\rightarrow \infty$ for negative energy $E$ . We now enforce the boundary condition that the wavefunction vanish in the region around $r=0$ where the potential goes to infinity, by

$F_2(r)=r^{\gamma}\xi, \quad \mbox{and set} \quad 2\sigma r=q$

to arrive at a hypergeometric equation

$}\Big(q\frac{d^2}{dq^2}+(2j+2-q)\frac{d}{dq}-(\frac{Ze^2E}{\sigma}-\gamma)\Big)\xi=0$

whose solution is well-described in “Special Functions” by N. N. Lebedev:
In order for the series solution to truncate to a polynomial we again find that

$\frac{Ze^2E}{\sigma}-\gamma=-N=0,1,2\cdots,$

$\frac{Ze^2E}{\sqrt{m^2-E^2}}=-N+\sqrt{(j+\frac{1}{2})^2-Z^2e^4}$

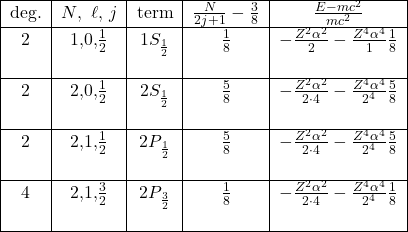
How good are these formulas? It is a simple exercise (you should do it!) to expand in powers of $e^2$ , (actually by restoring the appropriate $c$ and $\hbar$ factors, in powers of $\alpha={e^2\over \hbar c}\approx {1\over 137}$ )which is small