Physics 8xx: Green functions and contour integrals finale

How is the path integral used to compute $n$ -point functions? The LSZ formula tells us that they are what we need to compute amplitudes. Once again I follow Ramond’s “Field Theory, a Modern Primer”.
Introduce a driving force or current coupled $f(t)$ to the field,

$\langle q'(t)|q(T)\rangle=\int \mathcal{D}[q] e^{{i\over \hbar}\int_T^t dt\Big({1\over 2}\dot{q}^2-{1\over 2}\omega^2q^2+fq\Big)}$

Apply a convergence kludge to assuage any suspicions about convergence of the Gaussian integration

$\langle q'(t)|q(T)\rangle=\int \mathcal{D}[q] e^{{i\over \hbar}\int_T^t \Big({1\over 2}\dot{q}^2-{1\over 2}(\omega^2-i\epsilon)q^2+fq\Big)}$

and use the Fourier transform

$q(t)=\int_{-\infty}^\infty {d\xi\over \sqrt{2\pi}} e^{i\xi t} Q(\xi), \qquad Q(\xi)=\int_{-\infty}^\infty {dt\over \sqrt{2\pi}} e^{-i\xi t} q(t)$

$f(t)=\int_{-\infty}^\infty {d\xi\over \sqrt{2\pi}} e^{i\xi t} F(\xi), \qquad F(\xi)=\int_{-\infty}^\infty {dt\over \sqrt{2\pi}} e^{-i\xi t} f(t)$

This is a unitary transformation, so $\mathcal{D}[q]=\mathcal{D}[Q]$ . We can do the integrations in the exponent if $T\rightarrow -\infty$ and $t\rightarrow\infty$

(1) $\begin{eqnarray*}\int_{-\infty}^\infty dt\Big({1\over 2}\dot{q}^2+{1\over 2}(\omega^2-i\epsilon)q^2+Fq\Big)&=&\int_{-\infty}^\infty dt\int{d\xi \, d\xi'\over 2\pi}e^{i(\xi+\xi')t}\Big(-\Big({1\over 2}\xi\xi'-{1\over 2}(\omega^2-i\epsilon)\Big)Q(\xi)Q(\xi')\nonumber\\ &+&{1\over 2}\Big(F(\xi)Q(\xi')+F(\xi')Q(\xi)\Big)\Big)\nonumber\\ &=& \int d\xi \Big(-\Big(-{1\over 2}\xi^2-{1\over 2}(\omega^2-i\epsilon)\Big)Q(\xi)Q(-\xi)\nonumber\\ &+&{1\over 2}\Big(F(\xi)Q(-\xi)+F(-\xi)Q(\xi)\Big)\Big)\nonumber\end{eqnarray*}$

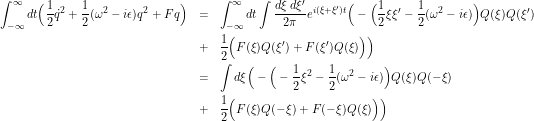
Change variables

$Q(\xi)\rightarrow Q(\xi)+{F(\xi)\over \xi^2-\omega^2+i\epsilon}$

in which you recognize the Green function for the oscillator, then

$\int_{-\infty}^\infty dt\Big({1\over 2}\dot{q}^2+{1\over 2}(\omega^2-i\epsilon)q^2+Fq\Big)$

$={1\over 2}\int d\xi \Big(Q(\xi)\Big(\xi^2-\omega^2 +i\epsilon\Big)Q(-\xi)-{F(\xi)F(-\xi)\over \xi^2-\omega^2+i\epsilon}\Big)$

and finally

(2) $\begin{eqnarray*}\langle q'(\infty)|q(-\infty)\rangle_{F\ne 0}&=&e^{-{i\over 2\hbar}\int d\xi {F(\xi)F(-\xi)\over \xi^2-\omega^2+i\epsilon}} \int \mathcal{D}[Q] e^{{i\over 2\hbar} \int d\xi Q(\xi)\Big(\xi^2-\omega^2 +i\epsilon\Big)Q(-\xi)}\nonumber\\ &=&e^{-{i\over 2\hbar}\int d\xi {F(\xi)F(-\xi)\over \xi^2-\omega^2+i\epsilon}}\langle q'(\infty)|q(-\infty)\rangle_{F=0}\nonumber\end{eqnarray*}$

Let’s get back into the time domain

(3) $\begin{eqnarray*}-\int d\xi {F(\xi)F(-\xi)\over \xi^2-\omega^2+i\epsilon}&=&\int_{-\infty}^\infty dt \, dt' \, \Big(-\int {d\xi\over 2\pi}{e^{-i\xi(t-t')}\over \xi^2-\omega^2+i\epsilon}\Big) F(t) \, F(t')\nonumber\\ &=& \int_{-\infty}^\infty dt \, dt' \, F(t) \, D(t-t') \, F(t')\nonumber\\ D(t-t') &=& -\int {d\xi\over 2\pi}{e^{-i\xi(t-t')}\over \xi^2-\omega^2+i\epsilon}\nonumber\end{eqnarray*}$

Note that

$\Big({d^2\over dt^2}+\omega^2\Big)D(t-t')=\int {d\xi\over 2\pi}e^{-i\xi(t-t')}{(\xi^2-\omega^2)\over \xi^2-\omega^2+i\epsilon}=\delta(t-t')$

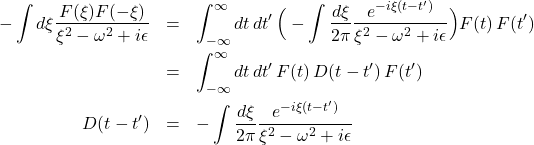
$\Big({d^2\over dt^2}+\omega^2\Big)\int_{-\infty}^\infty D(t-t')F(t') \, dt'=\int_{-\infty}^\infty \delta (t-t')F(t') \, dt'=F(t)$

This justifies it’s Green function name;

$q(t)=q_{hom}(t)+\int_{-\infty}^\infty D(t-t')F(t') \, dt'\quad\mbox{obeys}\quad \Big({d^2\over dt^2}+\omega^2\Big)q(t)=F(t)$

Heaviside step functions ( $\epsilon>0$ ) have integral representations

$e^{-i\omega(t-t')}\theta(t-t')=\frac{1}{2\pi i}\int d\xi\frac{e^{-i\xi(t-t')}}{\xi-\omega+i\epsilon}$

$e^{-i\omega(t'-t)}\theta(t'-t)=-\frac{1}{2\pi i}\int d\xi\frac{e^{-i\xi(t-t')}}{\xi+\omega-i\epsilon}$

obey $\theta(t-t')=1$ if $t\ge t'$ and is zero otherwise. You should prove that the integrals on the right sides of these formulas obey this relation, using the Cauchy theorem.

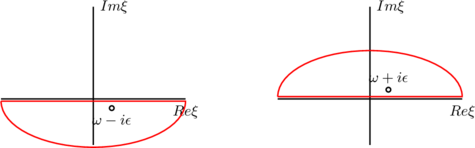
In the first integral we get a nonzero result iff we can complete the path of integration in the lower half-plane, requiring $e^{-i\xi(t-t')}\rightarrow 0$ for $\xi\rightarrow Re \, \xi-i\infty$ , which happens if $t>t'$ only. In the second integral we get a nonzero result iff we can complete the path of integration in the upper half-plane, requiring $e^{-i\xi(t-t')}\rightarrow 0$ for $\xi\rightarrow Re \, \xi+i\infty$ , which happens if $t<t'$ only. The Heaviside function is

$\theta(x-y)=\left\{\begin{array}{ll} 1 & x>y\\ 0 & x<y\end{array}\right.$

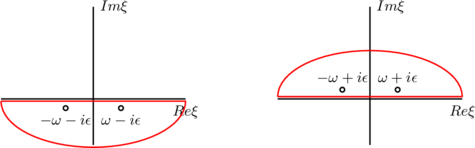
Explicitly evaluate $D_r$ ;

$D_r={2\pi i\over 2\pi } \Big({e^{-i(-\omega-i\epsilon)(t-t')}\over (-\omega-i\epsilon)-(\omega-i\epsilon)}+{e^{-i(\omega-i\epsilon)(t-t')}\over (\omega-i\epsilon)-(-\omega-i\epsilon)}\Big)\theta(t-t')$

$={\sin(\omega(t-t'))\over \omega}\theta(t-t')$

You can show that $D_a=-{\sin(\omega(t-t'))\over \omega}\theta(t'-t)$ , these are the usual oscillator retarded/advanced Green functions.
So what about $D(t-t')$ ? The poles are at

$0=\xi_p^2-\omega^2+i\epsilon, \qquad \xi_p=\pm \sqrt{\omega^2-i\epsilon}$

$=\omega-i{\epsilon\over 2\omega}=\omega-i\delta, \quad -\omega+i\delta, \quad \delta>0$

You can show that $D_a=-{\sin(\omega(t-t'))\over \omega}\theta(t'-t)$ , these are the usual oscillator retarded/advanced Green functions.\\
So what about $D(t-t')$ ? The poles are at

$0=\xi_p^2-\omega^2+i\epsilon, \qquad \xi_p=\pm \sqrt{\omega^2-i\epsilon}=\omega-i{\epsilon\over 2\omega}$

$=\omega-i\delta, \quad -\omega+i\delta, \quad \delta>0$

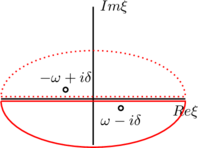
We can complete the contour in the lower half-plane when $t>t'$ so that $e^{-i(Re\omega+i Im \omega)(t-t')}\rightarrow e^{Im\omega(t-t')}\rightarrow 0$ as $Im\omega\rightarrow-\infty$ , contributing

$-{2\pi i\over 2}{e^{-i(\omega-i\delta)(t-t')}\over (\omega-i\delta)-(-\omega+i\delta)}\theta(t-t')$

$=-i{e^{-i\omega(t-t')}\over 2\omega}\theta(t-t')$

We can complete the contour in the upper half-plane when $t<t'$ so that $e^{-i(Re\omega+i Im \omega)(t-t')}\rightarrow e^{Im\omega(t-t')}\rightarrow 0$ as $Im\omega\rightarrow+\infty$ , contributing

${2\pi i\over 2}{e^{-i(-\omega+i\delta)(t-t')}\over (-\omega+i\delta)-(\omega-i\delta)}\theta(t'-t)=i{e^{i\omega(t-t')}\over 2\omega}\theta(t'-t)$

resulting in a mix of retarded/advanced signals

$D(t-t')={e^{-i\omega(t-t')}\over 2i\omega}\theta(t-t')+{e^{i\omega(t-t')}\over 2i\omega}\theta(t'-t)$

Ramond (which I am following closely) makes an interesting statement regarding this; “This is a precursor of the Feynmann propagator which describes signal propagation from two sources: positive energy (particle) states moving in positive time and negative energy (antiparticle) states moving backward in time”.

Notation;

$e^{-{i\over 2}\int dt_1 \int dt_2 F(t_1)D(t_1-t_2)F(t_2)}=W[F]=e^{iZ[F]}$

This is a generating function for $n$ -point functions.\\
$N$ -point functions. Starting with dividing $[t,t']$ into $N+1$ intervals $dt={t'-t\over N+1}$ , let $t''$ be somewhere on this interval,

(4) $\begin{eqnarray*}\langle q'(t')|q(t)\rangle&=&\int \mathcal{D}[q] e^{i\int_t^{t'} L(q,\dot{q}) dt}\nonumber\\ &=&\int \prod_{j=1}^N dq_j\langle q'|e^{-iH \, dt}|q_N\rangle\langle q_N|e^{-iH \, dt}|q_{N-1}\rangle\cdots \langle q_1|e^{-iH \, dt}|q\rangle\nonumber\\ \langle q'(t')|\hat{Q}(t'')|q(t)\rangle&=&\int \prod_{j=1}^N dq_j\langle q'|e^{-iH \, dt}|q_N\rangle\langle q_N|e^{-iH \, dt}|q_{N-1}\rangle\cdots \langle q_k|\hat{Q}e^{-iH \, dt}|q_{k-1}\rangle\cdots\langle q_1|e^{-iH \, dt}|q\rangle\nonumber\\ &=&\int \prod_{j=1}^N dq_j\langle q'|e^{-iH \, dt}|q_N\rangle\langle q_N|e^{-iH \, dt}|q_{N-1}\rangle\cdots q(t_k)\langle q_k|e^{-iH \, dt}|q_{k-1}\rangle\cdots\langle q_1|e^{-iH \, dt}|q\rangle\nonumber\\ &=&\int \prod_{j=1}^N dq_j \, q(t_k) \, \langle q'|e^{-iH \, dt}|q_N\rangle\langle q_N|e^{-iH \, dt}|q_{N-1}\rangle\cdots\langle q_k|e^{-iH \, dt}|q_{k-1}\rangle\cdots\langle q_1|e^{-iH \, dt}|q\rangle\nonumber\end{eqnarray*}$

(5) $\begin{eqnarray*}\langle q'(t')|q(t)\rangle &=& \int \mathcal{D}[q] \, q(t_k) \, e^{i\int_t^{t'} L(q,\dot{q}) dt}\nonumber\end{eqnarray*}$

…from which it should be clear from the expansion on the right-side that it is time ordered; pick two {\bf arbitrary times} $t_1,t_2$ , then each occurs at some multiple $k,\ell$ of $dt$ , $k>\ell$ ,

(6) $\begin{eqnarray*}&&\langle q'(t')|T\hat{Q}(t_1)\hat{Q}(t_2)|q(t)\rangle\nonumber\\ &= &\int \prod_{j=1}^N dq_j\langle q'|e^{-iH \, dt}|q_N\rangle\langle q_N|e^{-iH \, dt}|q_{N-1}\rangle\cdots \langle q_k|\hat{Q}e^{-iH \, dt}|q_{k-1}\rangle\cdots\langle q_\ell|\hat{Q}e^{-iH \, dt}|q_{\ell-1}\rangle\cdots\langle q_1|e^{-iH \, dt}|q\rangle\nonumber\\ &= &\int \prod_{j=1}^N dq_j\langle q'|e^{-iH \, dt}|q_N\rangle\langle q_N|e^{-iH \, dt}|q_{N-1}\rangle\cdots q(t_k)\langle q_k|e^{-iH \, dt}|q_{k-1}\rangle\cdots q(t_\ell)\langle q_\ell|e^{-iH \, dt}|q_{\ell-1}\rangle\cdots\langle q_1|e^{-iH \, dt}|q\rangle\nonumber\\ &=& \int \mathcal{D}[q] \, q(t_1) q(t_2)\, e^{i\int_t^{t'} L(q,\dot{q}) dt}\nonumber\end{eqnarray*}$

so the object on the right automatically produces time ordered operator product amplitudes.
Introduce variational derivatives

${\delta\over \delta f(x)}f(y)=\delta(x-y), \qquad {\delta\over \delta f(x)}\int f(y) K(y) \, dy=K(x)$

and returning momentarily to the oscillator
$begin{eqnarray}{\delta\over \delta f(t)}e^{-{i\over 2}\int dt_1 \int dt_2 F(t_1)D(t_1-t_2)F(t_2)}&=&-{i\over 2}\Big(\int dt_1 \int dt_2 \Big(\delta(t-t_1)D(t_1-t_2)F(t_2)\nonumber\\ &+&F(t_1)D(t_1-t_2)\delta(t-t_2)\Big)e^{-{i\over 2}\int dt_1 \int dt_2 F(t_1)D(t_1-t_2)F(t_2)}\nonumber\\ &=&-i\int dt_1D(t-t_1)F(t_1)\, \, e^{-{i\over 2}\int dt_1 \int dt_2 F(t_1)D(t_1-t_2)F(t_2)}\nonumber\\ {\delta^2\over \delta f(t) \delta(t')}e^{-{i\over 2}\int dt_1 \int dt_2 F(t_1)D(t_1-t_2)F(t_2)}\Big{|}_{F=0}&=&-iD(t-t')\nonumber\end{eqnarray}$

Let $H\rightarrow H'=H-fq$ where $f(t)$ is some force or current, then with $t_1=k\delta t$ and $t_2=\ell dt$ , $\ell<k$ , the variational derivatives will ignore all functions of $t$ for which $t\ne t_1,t_2$ in

(7) $\begin{eqnarray*}&&{\delta\over \delta f(t_1)}{\delta\over \delta f(t_1)}\langle q'(t')|q(t)\rangle\nonumber\\ &= &\int \prod_{j=1}^N dq_j\langle q'|e^{-iH' \, dt}|q_N\rangle\langle q_N|e^{-iH' \, dt}|q_{N-1}\rangle\cdots {\delta\over \delta f_k}\langle q_k|e^{-iH' \, dt}|q_{k-1}\rangle\nonumber\\ &\cdots&{\delta\over \delta f_\ell}\langle q_\ell|e^{-iH' \, dt}|q_{\ell-1}\rangle\cdots\langle q_1|e^{-iH' \, dt}|q\rangle\nonumber\\ &= &i^2\int \prod_{j=1}^N dq_j\langle q'|e^{-iH' \, dt}|q_N\rangle\langle q_N|e^{-iH' \, dt}|q_{N-1}\rangle\cdots q(t_k)\langle q_k|e^{-iH' \, dt}|q_{k-1}\rangle\nonumber\\ &\cdots& q(t_\ell)\langle q_\ell|e^{-iH' \, dt}|q_{\ell-1}\rangle\cdots\langle q_1|e^{-iH' \, dt}|q\rangle\nonumber\\ &=& i^2\int \mathcal{D}[q] \, q(t_1) q(t_2)\, e^{i\int_t^{t'} (L(q,\dot{q})+fq) dt}\nonumber\end{eqnarray*}$

from which you can see that the path integral generates time-ordered expectations of operator products for $H\rightarrow H'=H-fq$

${\delta\over \delta f(t_1)}\cdots {\delta\over \delta f(t_n)}\langle q'(t')|q(t)\rangle\Big{|}_{f=0}=\langle q'(t')|T\hat{Q}(t_1)\hat{Q}(t_2)|q(t)\rangle$

At $t\rightarrow\pm\infty$ assume that the sources/drivers are zero, let $|0_{\pm\infty}\rangle$ be the ground/vacuum states at these times and we are using $\omega^2\rightarrow \omega^2-i\epsilon$ ;

(8) $\begin{eqnarray*}\langle 0_\infty|0_{-\infty}\rangle_{F\ne 0}&=& \int dq' dq \langle 0_\infty|q'_\infty\rangle\langle q'_\infty|q_{-\infty}\rangle_{F\ne 0}\langle q_{-\infty}|0_{-\infty}\rangle\nonumber\\ &=& \int dq' dq \langle 0_\infty|q'_\infty\rangle e^{-{i\over 2\hbar}\int d\xi {F(\xi)F(-\xi)\over \xi^2-\omega^2+i\epsilon}}\langle q'(\infty)|q(-\infty)\rangle_{F=0}\, \langle q_{-\infty}|0_{-\infty}\rangle\nonumber\\ &=& \Big(\int dq' dq \langle 0_\infty|q'_\infty\rangle \langle q'(\infty)|q(-\infty)\rangle_{F=0}\, \langle q_{-\infty}|0_{-\infty}\rangle\Big)e^{-{i\over 2\hbar}\int d\xi {F(\xi)F(-\xi)\over \xi^2-\omega^2+i\epsilon}} \nonumber\\ &=& \langle 0_\infty|0_{-\infty}\rangle_{F=0} \, e^{-{i\over 2\hbar}\int d\xi {F(\xi)F(-\xi)\over \xi^2-\omega^2+i\epsilon}} \nonumber\\ &=& \langle 0_\infty|0_{-\infty}\rangle_{F=0} e^{-{i\over 2}\int dt_1 \int dt_2 F(t_1)D(t_1-t_2)F(t_2)}\nonumber\\ &=& \langle 0_\infty|0_{-\infty}\rangle_{F=0} \int \mathcal{D}[q] e^{i\int_{-\infty}^\infty \Big({1\over 2}\dot{q}^2-{1\over 2}(\omega^2-i\epsilon)q^2+fq\Big)}\nonumber\end{eqnarray*}$

Without sources/drivers $\langle 0_\infty|0_{-\infty}\rangle_{F=0}=1$ . All of the following are equivalent

(9) $\begin{eqnarray*}\int \mathcal{D}[q] e^{i\int_{-\infty}^\infty \Big({m\over 2}\dot{q}^2-{1\over 2}m(\omega^2-i\epsilon)q^2+fq\Big)}&=&e^{-{i\over 2\hbar}\int d\xi {F(\xi)F(-\xi)\over \xi^2-\omega^2+i\epsilon}} \nonumber\\ \int \mathcal{D}[q] e^{i\int_{-\infty}^\infty \Big({m\over 2}(1+i\epsilon)\dot{q}^2-{1\over 2}m(1-i\epsilon)\omega^2q^2+fq\Big)}&=&e^{-{i\over 2\hbar}\int d\xi {F(\xi)F(-\xi)\over \xi^2-\omega^2+i\epsilon}} \nonumber\\ \int \mathcal{D}[q] \mathcal{D}[p]e^{i\int_{-\infty}^\infty \Big(p\dot{q}-(1-i\epsilon)H+fq\Big)}&=&e^{-{i\over 2\hbar}\int d\xi {F(\xi)F(-\xi)\over \xi^2-\omega^2+i\epsilon}} \nonumber\end{eqnarray*}$

provided factors like $\omega^2, (\xi^2+\omega^2)$ are absorbed into $\epsilon$ .

Home 2.0

Physics 8xx: Green functions and contour integrals finale

Related Posts

Physics 8xx: Green functions and contour integrals finale

Published by Jeff on December 6, 2021December 6, 2021

Related Posts

Protected: Physics 715 : Landau theory of phase transitions

Protected: Physics 715: Lee-Yang theory of phase transitions

Protected: Physics 715: Ising model in one dimension