Green functions are used to solve inhomogeneous versions of differential equations whose homogeneous versions we have solved with Laplace transformation. Consider a classical harmonic oscillator that begins undisplaced and at rest before ![]() . It is then subjected to an arbitrary force
. It is then subjected to an arbitrary force
![]()
If there is such a function ![]() ;
;
![]()
![]()
satisfies our Newtonian equation of motion, with ![]() being a solution to the homogeneous equation with
being a solution to the homogeneous equation with ![]() .
.
The delta function represents an impulse applied to the object, and any force can be represented as a suitably tuned set of impulses, since
![]()
To see how this works apply ![]()
to both sides of the equation,
![]()
![]()
We solve using Laplace transformation, the most sophisticated tool for solving EOMs used in Physics 311. Call ![]() , and use
, and use
![]()
Then
![]()
We work out thi inverse transformation by simply fishing for it rather than digress into Laplace transformations, so we make an inspired guess based on the idea of causality: nothing should respond to the force/impulse until after it is applied. Therefore consider that a particle has displacement
![]()
(1) 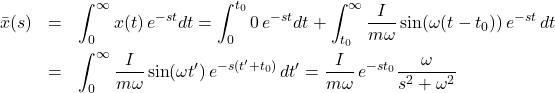
so that we can conclude that for the oscillator (set ![]() )
)
![]()
In classical mechanics we use Laplace transforms to solve second order EOMs with initial data for ![]() and
and ![]() . In electrodynamics we are concerned with waves, and so Fourier transformation is more appropriate. Let’s do the same problem (impacted oscillator) with Fourier transformation and see how causality is enforced in that scenario.
. In electrodynamics we are concerned with waves, and so Fourier transformation is more appropriate. Let’s do the same problem (impacted oscillator) with Fourier transformation and see how causality is enforced in that scenario.
Start again with
![]()
![]()
![]()
![]()
it works out, since
![]()
but there is no hint of causality: the fact that there must be no response before the effect that causes it.
Contour integration evaluation of the Green function fixes this.
If you put this back into the formula for ![]() , the results are a clearly divergent or improper integral
, the results are a clearly divergent or improper integral
![]()
We make sense of this by thinking of ![]() as being potentially complex, and we alter the kernel\index{impulses}
as being potentially complex, and we alter the kernel\index{impulses}
![]()
in such a way as to {\bf enforce causality: no response to the force before it is applied}. This can be accomplished by altering the the kernel as
![]()
![]()
and the integral must now be performed in the complex ![]() plane.
plane.

If we do so, then the integral for the green function is not only convergent, but enforces causality
![]()
a result that we obtain by Cauchy’s theorem. If ![]() then in the upper half-plane
then in the upper half-plane
![]()
and I complete the integral contour ![]() with the blue arc at infinity (on which the integrand is zer) and obtain just
with the blue arc at infinity (on which the integrand is zer) and obtain just ![]() times the sum of the residues
times the sum of the residues
![]()
![]()
If ![]() I must complete it on the red arc, surrounding no poles, obtaining zero.
I must complete it on the red arc, surrounding no poles, obtaining zero.
The heaviside step function is defined by
![]()
![]()
and has a few useful properties by virtue of simply evaluating to zero or one, one of which is
![]()
![]()
to be contrasted with the delta function scaling behaviour
![]()
We (I mean you) will use this as well in the near future.
Electrodynamic potential
Start with our equation for the scalar potential in the Lorentz gauge
![]()
and suppose that both ![]() and
and ![]() have Fourier expansions
have Fourier expansions
![]()
![]()
and inverses
![]()
![]()
substitute these into each side of the wave equation and notice that waves of different frequencies in either ![]() or
or ![]() domain are linearly independent on the interval
domain are linearly independent on the interval ![]() , and so the coefficients of the different components
, and so the coefficients of the different components ![]() must match
must match
![]()
One of the most useful cases is for the “charge density” (an electromagnetic “instanton”)
![]()
(although ![]() would represent an actual {\bf charge} blinking into/out of existence) resulting in the Green function
would represent an actual {\bf charge} blinking into/out of existence) resulting in the Green function
![]()
and we invert the transformation to get the potential
![]()
Let’s orient the ![]() -system so that its
-system so that its ![]() axis points along
axis points along ![]() and assume
and assume ![]() ;
;
(2) 
In the second integral of the second from last line
![]()
do the transformation ![]() ,
,
![]()
![]()
so the entire second from last line becomes
![]()
![]()
Similarly with the first integral in the last line
![]()
![]()
![]()
so the last line becomes
![]()
![]()
(3) 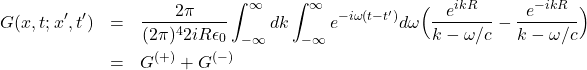
So far we have done nothing special, just a few variable changes and the angular integrals.
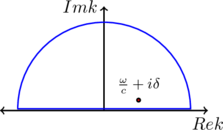
To do the ![]() -integral; we add a small imaginary part to
-integral; we add a small imaginary part to ![]() ,
,
![]()
to the integral, then let this quantity go back to zero. When I do the ![]() -integral, I can close the contour in the upper-half plane since there
-integral, I can close the contour in the upper-half plane since there
![]()
and in this case we will only surround the pole in the parenthesis and obtain
![]()
![]()
carefully counting up all of the ![]() ‘s and
‘s and ![]() ‘s. Similarly
‘s. Similarly
![]()
![]()
![]() is the scalar potential of a point charge at
is the scalar potential of a point charge at ![]() as it existed for an instant at
as it existed for an instant at ![]() .
.
Note that these are our usual Green functions ![]() for
for ![]()
![]()
but they are modified by a factor that (in the case of the retarded version) enforces causality, the potential felt at ![]() at
at ![]() was the one created by the particle source when it was at
was the one created by the particle source when it was at ![]() at
at ![]() with
with ![]() .
.