In Memoriam: Dirac theory

My thesis advisor Adam Bincer gave marvelous lectures in 732 and 831 on the Dirac equation. I took 831 in 1979 (no, it was 1980) from him as a college junior, a happy chemistry major. His influence was so strong that two days into the semester I decided to switch to physics for graduate school.
I am so glad that in those days we students took meticulous notes on paper, so that I can share them with you today…

If we simply wish to force the Schrodinger equation to comply with relativity then a simple replacement of the kinetic energy

$T=\frac{\mathbf{p}^2}{2m} \quad\mbox{with the relativistic counterpart}\quad T=\sqrt{\mathbf{p}^2c^2+m^2c^4}-mc^2$

should suffice. So one could be led to believe. This introduces correction terms into the Hamiltonian for an atom that we can handle using perturbation theory

$H=mc^2+\frac{\mathbf{p}^2}{2m}-\frac{\mathbf{p}^4}{8m^3c^2}+\cdots -mc^2 +V(r)$

and replacement of the dynamical variables with quantum operators via the canonical quantization procedure (equivalent to replacing Poisson brackets with commutators)

$E\rightarrow i\hbar\frac{\partial}{\partial t}, \qquad \mathbf{p}\rightarrow -i\hbar \bm{\nabla}$

results in the Klien-Gordon wave equation.

$\Big(\hbar^2(\frac{\partial^2}{\partial t^2}-c^2\bm{\nabla}^2)+m^2c^4\Big)\psi=0$

Unfortunately the positive-definite quantity $\psi^{*}\psi$
no longer occurs in the “probability flux conservation law”

$\frac{\partial\rho}{\partial t}+\bm{\nabla}\cdot \mathbf{S}=0, \quad \mbox{with}\quad \mathbf{S}=\frac{1}{2m}(\psi^{*}\bm{\nabla}\psi-(\bm{\nabla}\psi^{*})\psi)$

It is trivial to show that for the Klien-Gordon equation

$\mathbf{S}=\frac{1}{i}(\psi^{*}\bm{\nabla}\psi-(\bm{\nabla}\psi^{*})\psi)\quad\mbox{and} \quad \rho=i(\psi^{*}\frac{\partial\psi}{\partial t}-\frac{\partial \psi^{*}}{\partial t}\psi)$

obeys

$\frac{\partial\rho}{\partial t}+\bm{\nabla}\cdot \mathbf{S}=0$

but this $\rho$ is not always positive, and therefore cannot be interpreted as a probability density. We certainly want probabilities of finding particle in any region to be positive or zero. We can get around this by interpreting this quantity as a charge density instead, but that doesn’t let us use it as a probability, so that functionality is lost, which breaks the measurement theory of the system. This is not the only problem. If we look for solutions such as

$\psi=Ne^{-i\frac{Et-px}{\hbar}} \quad\mbox{we find that}\quad E=\pm \sqrt{\mathbf{p}^2c^2+m^2c^4}, \qquad \rho=2E|N|^2$

and so we have negative energy states! Furthermore the negative energy states have a negative probability density. Since $|E|>mc^2$ the positive energy states all have positive $\rho$ and the negative energy states all have negative $\rho$ . As far as Fourier analysis is concerned this is no problem, we simply have two Hilbert spaces that with proper choice of norm can be made disjoint and orthogonal. The negative energy states do pose a stability problem, since the energy can be arbitrarily large and negative the theory has no stable ground state.

The current for these plane wave states can be seen to be

$S^{\mu}=2p^{\mu}|N|^2$

where the index $\mu$ can be $1, 2, 3, 0$ , meaning $x, y, z$ , and $t$ respectively with $p^0=E$ . Therefore $\rho$ is the time component of the relativistic current four vector. Normalization of these relativistic states is a trickier matter. Recall that

$|\psi(x)|^2 \, d^3x$

must be the probability of finding the particle in a small volume in a particular location $x$ . If we Lorentz boost into another frame moving parallel to the $x$ -axis at $v$ then

$dx \, dy \, dz \rightarrow dx' \, dy' \, dz' =\sqrt{1-v^2} \, dx \, dy \, dz$

and in order to keep the probability the same in that volume for all observers the $\gamma$ factor must be compensated for.

Fortunately $\rho$ contains a hint; normalize so that there are $2E$ particles per unit volume so that

$2E \, dx \, dy \, dz \rightarrow 2E' \, dx' \, dy' \, dz'=2\gamma E \gamma^{-1} \, dx \, dy \, dz =2E \, dx \, dy \, dz$

and so we choose $N=1$ so that

$\int \rho \, dx \, dy \, dz =2E$

where we have calibrated the volume of all of space to be one. This is legal since any scattering results must be volume independent anyway.

Since the square root operator appears to be the source of all evil, Dirac proposed a linear wave equation in order to avoid it. He suggested the form

$i \, \frac{\partial \psi}{\partial t}=(-i\bm{\alpha}\cdot \bm{\nabla}+\beta m)\psi$

where from now on we will take $c=1$ . In order that this comform to the requirements of relativity we must have
$\bullet$ The square of the operator acting on $\psi$ must be the same as the Klein-Gordon equation.
$\bullet$ There must exist a positive probability density $\rho$ such that

$\dot{\rho}+\bm{\nabla}\cdot\mathbf{S}=0$

We want an intact measurement theory.
$\bullet$ The operators $\bm{\alpha}$ and $\beta$ can have no coordinate or momentum dependence.
Requirement one means that

$(-i\bm{\alpha}\cdot\bm{\nabla}+\beta m)^2=(-\nabla^2 +m^2)$

which after the operator substitution $-i\bm{\nabla}=\mathbf{P}$ becomes

$(\alpha_xP_x+\alpha_yP_y+\alpha_zP_z +\beta m)^2=(P_x^2+P_y^2+P_z^2+m^2)$

If we define the

$\{A,B\}=AB+BA$

we see that these relations can be met by

$\{\alpha_x,\alpha_y\}=\{\alpha_x,\alpha_z\}=\{\alpha_y,\alpha_z\}=0, \qquad \{\beta,\alpha_x\}=\{\beta,\alpha_y\}=\{\beta,\alpha_z\}=0$

and

$\beta^2=\alpha_x^2=\alpha_y^2=\alpha_z^2=1$

It should be fairly clear that no numbers satisfy these requirements (these are the algebraic rules of a Clifford algebra) We have three matrices that satisfy these relations

$\sigma_x=\left(\begin{array}{cc} 0 & 1\\ 1 & 0\end{array}\right), \quad\sigma_y=\left(\begin{array}{cc} 0 & -i\\ i & 0\end{array}\right), \quad \sigma_z=\left(\begin{array}{cc} 1 & 0\\ 0 & -1\end{array}\right)$

$\{\sigma_i,\sigma_j\}=2\delta_{i,j}$

However we need four such objects, not three. It is easy to show that

$\alpha_x=\left(\begin{array}{cc} 0&\sigma_x\\\sigma_x&0\end{array}\right), \quad \alpha_y=\left(\begin{array}{cc} 0&\sigma_y\\\sigma_y&0\end{array}\right), \quad \alpha_z=\left(\begin{array}{cc} 0&\sigma_z\\\sigma_z&0\end{array}\right)$

$\beta=\left(\begin{array}{cc}1&0\\0&-1\end{array}\right)$

where the “ $1$ ” means a $2\times 2$ unit matrix, satisfies all of the required algebraic relations. It appears that simply satisfying relativistic requirements is intimately tied up with spin. The Dirac equation is therefore a matrix equation whose eigenstates are spinors, irreducible representations of a Clifford algebra.

$\left(\begin{array}{cccc}m&0&P_z&-iP_y+P_x\\0&m&iP_y+P_x&-P_z\\P_z&-iP_y+P_x&-m&0\\iP_y+P_x&-P_z&0&-m\end{array}\right)\left(\begin{array}{c}\psi_1\\\psi_2\\\psi_3\\\psi_4\end{array}\right)=i\frac{\partial}{\partial t}\left(\begin{array}{c}\psi_1\\\psi_2\\\psi_3\\\psi_4\end{array}\right)$

We solve this first for the relativistic plane wave states

$\psi_j=e^{i\mathbf{p}\cdot\mathbf{r}-Et} \, \chi_j, \quad j=1,2,3,4$

results in four linear equations for the four components (not space-time components, something quite new) $\chi_1, \chi_2, \chi_3, \chi_4$ which have a solution if the determinant

$\left|\begin{array}{cccc}m-E&0&P_z&-iP_y+P_x\\0&m-E&iP_y+P_x&-P_z\\P_z&-iP_y+P_x&-m-E&0\\iP_y+P_x&-P_z&0&-m-E\end{array}\right|=0$

from which we find

$E^2=\mathbf{p}^2 +m^2$

which was a requirement laid down by Dirac. We can procede to find the actual spinors by defining

$\chi=\left(\begin{array}{c}\chi_1\\\chi_2\end{array}\right), \qquad \phi=\left(\begin{array}{c}\chi_3\\\chi_4\end{array}\right)$

Then we find that

$-(m-E)\chi=(\mathbf{p}\cdot\bm{\sigma})\phi, \qquad (m+E)\phi=(\mathbf{p}\cdot\bm{\sigma})\chi$

We now choose

$\phi=\phi_\uparrow=\left(\begin{array}{c}1\\0\end{array}\right), \quad\mbox{or}\quad \phi=\phi_\downarrow=\left(\begin{array}{c}0\\1\end{array}\right)$

We see that there will be four solutions, what do they describe? A spin one-half electron only needs two degrees of freedom, so clearly these have more structure than we need. To find out what these wavefunctions represent, multiply the Dirac equation by $\beta$ from the left

$(-i\beta \frac{\partial}{\partial t}-i\beta\bm{\alpha}\cdot \bm{\nabla}+m)\psi=0$

and define the four-vector (which {\bf is} a space-time four-vector)

$\gamma^{\mu}=\left(\begin{array}{c}\gamma^0\\ \gamma^1\\ \gamma^2\\ \gamma^3\end{array}\right)=(\beta,\beta\bm{\alpha})^T$

and we obtain a form of the Dirac equation that does not distinguish $t$ from any other coordinate (the covariant form)

$(i\gamma^{\mu}\partial_{\mu} -m)\psi=0$

where we make the short-hand notation $\partial_{\mu}=\frac{\partial}{\partial x_{\mu}}$
with $\mu=0$ denoting $t$ , $\mu=1$ denoting $x$ , and so forth, and we sum over repeated indices so that

$A^{\mu}B_{\mu}=A^0B_0+A^1B_1+A^2B_2+A^3B_3=A^0B^0-(A^1 B^1+A^2 B^2+A^3 B^3)$

In space-time (Minkowski space) we distinguish between upper (contravariant) and lower (covariant)indices, and translate between them with a metric tensor $g$

$g=\left(\begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & -1\end{array}\right)$

$x_\mu=g^{\mu, \nu} x_\nu, \quad A^\mu B_\mu=g^{\mu, \nu} A_\mu B_\nu$

$x^\mu=(t,x,y,z)^T, \quad x_\mu=(t,-x,-y,-z), \quad \partial_\mu={\partial\over \partial x^\mu}=(\partial_t,\partial_x,\partial_y,\partial_z)$

The Dirac matrices satisfy

$\{\gamma^{\mu},\gamma^{\nu}\}=2\delta^{\mu\nu}$

also the action of conjugation can be accomplished with

$(\gamma^{\mu})^{\dagger}=\beta \gamma^{\mu}\beta=\gamma^0\gamma^{\mu}\gamma^0 =-\gamma^{\mu}, \quad \mu=1,2,3, \qquad (\gamma^0)^{\dagger}=\gamma^0$

which you should verify. Recall the basic matrix manipulations

$(AB)^T=B^TA^T, \qquad (AB)^{\dagger}=B^{\dagger}A^{\dagger}$

At any rate these relations can be used to obtain the probability and currents that we need to construct a meaningful theory.

Conjugation of the Dirac equation leads to a form

$-i\frac{\partial \psi^{\dagger}}{\partial t}\gamma^0+i\bm{\nabla}\psi^{\dagger}\cdot(\bm{\gamma}^{\dagger})-m\psi^{\dagger}=0$

$-i\frac{\partial \psi^{\dagger}}{\partial t}\gamma^0-i\bm{\nabla}\psi^{\dagger}\cdot\bm{\gamma}-m\psi^{\dagger}=0$

with different signs for the time and spatial derivative terms. Since

$\{\gamma^{j},\gamma^0\}=0$

multiplication on the right by $\gamma^0$ and moving $\gamma^0$ through $\vec{\gamma}$ results in a covariant form

$i\partial_{\mu}\bar{\psi}\gamma^{\mu}+m\bar{\psi}=0$

where

$\bar{\psi}=\psi^{\dagger}\gamma^0$

which is called the adjoint spinor to distinguish it from the simple conjugate. Multiply the Dirac equation on the left by the adjoint spinor and the adjoint equation on the right by $\psi$ and subtract to obtain the desired current conservation law

$\partial_t(\bar{\psi}\gamma^0\psi)+\bm{\nabla}\cdot(\bar{\psi}\bm{\gamma}\psi)=0$

which has a probability density that is manifestly positive (so a big win here).

$\rho=\bar{\psi}\gamma^0\psi=\psi^{\dagger}\psi=\sum_{i=i}^4|\psi_i|^2,\qquad \mathbf{S}=\bar{\psi}\bm{\gamma}\psi$

What do the Dirac states represent?
We now re-interpret the spectrum of the Dirac theory. Return to

$\psi=e^{i(\mathbf{p}\cdot \mathbf{r}-Et)} \, \left(\begin{array}{c} \chi \\ \phi\end{array}\right), \qquad -(m-E)\chi=(\mathbf{p}\cdot\bm{\sigma})\phi$

$(m+E)\phi=(\mathbf{p}\cdot\bm{\sigma})\chi$

We now choose

$\chi=\chi_\uparrow=\left(\begin{array}{c}1\\0\end{array}\right), \quad\mbox{or}\quad \chi=\chi_\downarrow=\left(\begin{array}{c}0\\1\end{array}\right)$

and get the corresponding $\phi$ object from one of these equations

$\psi=e^{i(\mathbf{p}\cdot \mathbf{r}-Et)} \, \left(\begin{array}{c} \chi_{\uparrow, \downarrow} \\ {1\over (E+m)}\mathbf{p}\cdot\bm{\sigma} \, \chi_{\uparrow, \downarrow}\end{array}\right)\rightarrow e^{i(\mathbf{p}\cdot \mathbf{r}-Et)} \, \left(\begin{array}{c} \chi_{\uparrow, \downarrow} \\ 0\end{array}\right), \quad |\mathbf{p}|\rightarrow 0$

These states will be shown to represent spin up/down (meaning the $z$ -component of angular momentum in the rest frame is $\pm \tfrac{1}{2} \hbar$ ), and make sense for $E>0$ , since if $E<0$ the two lower components would blow up rather than vanish in the rest frame. We calculate $\Big({\mathbf{p}\cdot\bm{\sigma}\over E+m}\Big)^2={\mathbf{p}\cdot\mathbf{p}\over(E+m)^2}={E-m\over E+m}\rightarrow 0$ as $|\mathbf{p}|\rightarrow 0$ .
There are two other linearly independent solutions. Pick

$\phi=\phi_\uparrow=\left(\begin{array}{c}1\\0\end{array}\right), \quad\mbox{or}\quad \phi=\phi_\downarrow=\left(\begin{array}{c}0\\1\end{array}\right)$

and get the corresponding $\chi$ object from the other equation

$\psi=e^{i(\mathbf{p}\cdot \mathbf{r}-Et)} \, \left(\begin{array}{c} {1\over (E-m)}\mathbf{p}\cdot\bm{\sigma} \, \phi_{\uparrow, \downarrow}\\ \phi_{\uparrow, \downarrow} \\ \end{array}\right)$

This pair of solutions only makes sense if $E<0$ , since $\Big({\mathbf{p}\cdot\bm{\sigma}\over E-m}\Big)^2={\mathbf{p}\cdot\mathbf{p}\over(E-m)^2}={E+m\over E-m}$ , which blows up in the nonrelativistic limit if $E>0$ , and so we have not escaped the negative energy problem.

We have four linearly independent solutions, and the spinor portions of the respective wavefunctions are

$\left(\begin{array}{c}\left(\begin{array}{c}1\\0\end{array}\right)\\\frac{\mathbf{p}\cdot\bm{\sigma}}{E+m}\left(\begin{array}{c}1\\0\end{array}\right)\end{array}\right)=u^{(1)}, \quad \left(\begin{array}{c}\left(\begin{array}{c}0\\1\end{array}\right)\\\frac{\mathbf{p}\cdot\bm{\sigma}}{E+m}\left(\begin{array}{c}0\\1\end{array}\right)\end{array}\right)=u^{(2)}$

$\left(\begin{array}{c}\frac{-\mathbf{p}\cdot\bm{\sigma}}{|E|+m}\left(\begin{array}{c}1\\0\end{array}\right)\\\left(\begin{array}{c}1\\0\end{array}\right)\end{array}\right)=u^{(3)}, \quad \left(\begin{array}{c}\frac{-\mathbf{p}\cdot\bm{\sigma}}{|E|+m}\left(\begin{array}{c}0\\1\end{array}\right)\\\left(\begin{array}{c}0\\1\end{array}\right)\end{array}\right)=u^{(4)}$

The first two are positive energy, and the second two are negative energy. We will interpret the spin-up, spin-down components of the electron wavefunction to be

$\psi_{electron, E, s, \mathbf{p}}(\mathbf{r}, t)=u^{(1,2)}(\mathbf{p}) \, e^{i(\mathbf{p}\cdot \mathbf{r}-Et)}$

$s=\uparrow \, (u^{(1)}), \qquad s=\downarrow \, (u^{(2)}), \quad E>0$

and the other two components to represent the anti-electron. Unfortunately since the spectrum has no lowest state, there will be no stable states for one particle systems. We will later prove that the electron obeys the Pauli Exclusion Principle; one or no particles per quantum state. Our quantum states are labeled by spin up/down and the energy.

If we think of a “naive” vacuum $|0\rangle_{naive}$ as a state containing none of these particle states and invent creation operators $\hat{c}_k^{(i)\dagger}$ , $i=1,2,3,4$ then there are positive and negative energy excitations.

$\hat{c}_k^{(1)\dagger}|0\rangle_{naive}, \quad \hat{c}_k^{(2)\dagger}|0\rangle_{naive}$

create positive energy excitation associate with wavefunctions

$u^{(1)}_k \, e^{i(\mathbf{k}\cdot\mathbf{x}-Et)}, \quad u^{(2)}_k \, e^{i(\mathbf{k}\cdot\mathbf{x}-Et)}$

However

$\hat{c}_k^{(3)\dagger}|0\rangle_{naive}, \quad \hat{c}_k^{(4)\dagger}|0\rangle_{naive}$

create negative energy $E=-|E|$ excitation associate with wavefunctions

$u^{(3)}_k \, e^{i(\mathbf{k}\cdot\mathbf{x}+|E|t)}, \quad u^{(4)}_k \, e^{i(\mathbf{k}\cdot\mathbf{x}+|E|t)}$

This will result in a sort of negative-feedback in which any interactions will stimulate the production of negative energy states in an effort to descend into a ground state, which is lower in energy than the $|0\rangle_{naive}$ state.

The figure above illustrates such a negative energy, spin-down state

$\hat{c}_k^{(4)\dagger}|0\rangle_{naive}, \quad\mbox{of wavefunction} \quad u^{(4)}_k \, e^{i(\mathbf{k}\cdot\mathbf{x}+|E|t)}$

Dirac solved the instability problem by reinventing the concept of vacuum. The vacuum (lowest energy state)consists of the state with all negative energy levels filled. This is called the Dirac sea, and we will denote it by $|0\rangle$ .

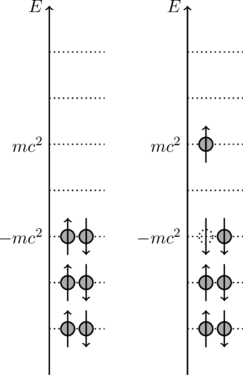
We define the energy of this to be zero, and its momentum, charge, and spin to be zero as well and measure the quantum numbers of all states relative to this zero point.
Note that (once we establish the exclusion principle)

$\hat{c}_k^{(3)\dagger} \, |0\rangle=\hat{c}_k^{(4)\dagger} \, |0\rangle=0, \quad \forall k$

since all negative energy states are already filled!

Antiparticles.of greater significance is that

$\hat{c}_k^{(3)} \, |0\rangle$

is a hole in the vacuum, subtracting a negative energy, a momentum $\mathbf{k}$ and an up-spin from the vacuum. This “hole” in the vacuum can be thought of as an excitation created by a “hole creation” operator

$\hat{c}_k^{(3)} \, |0\rangle=\hat{d}_{-k}^{(2)\dagger} \, |0\rangle$

producing a spin-down, positive energy state (the dotted circle).

If the states created by $\hat{c}_k^{(1,2)\dagger}$ are electrons, this hole is the anti-electron, called a positron. It is a positive energy excitation

$\hat{c}_{k}^{(3)} |0\rangle=\hat{d}_{-k}^{(2)\dagger} |0\rangle$

$\mbox{wavefunction} \quad \psi_{positron, E, \downarrow, -\mathbf{k}}=v^{(2)}(-\mathbf{k}) \, e^{-ik\cdot x}=u^{(3)}(\mathbf{k}) \, e^{i(-\mathbf{k}\cdot \mathbf{x}-|E|t)}$

$\hat{c}_{k}^{(4)} |0\rangle=\hat{d}_{-k}^{(1)\dagger} |0\rangle$

$\mbox{wavefunction} \quad \psi_{positron, E, \uparrow, -\mathbf{k}}=v^{(1)}(-\mathbf{k}) \, e^{-ik\cdot x}=u^{(4)}(\mathbf{k}) \, e^{i(-\mathbf{k}\cdot \mathbf{x}-|E|t)}$

(remember that $u^{(3,4)}_k$ Dirac solutions had $e^{i(\mathbf{k}\cdot\mathbf{x}-(-|E|)t)}$ wavefunctions). and its wavefunction is

$\psi_{positron, E, s, \mathbf{p}}=v^{(1,2)}(\mathbf{p}) \, e^{ip\cdot x}=u^{(4,3)}(-\mathbf{p}) \, e^{-i(-p)\cdot x}, \quad s=\uparrow (1), \quad s=\downarrow (2)$

Schrodinger wrote down the wave equation in 1926. Dirac wrote his down in 1928, and by 1932 anti-electrons were detected and identified in cloud chambers.

We also need to normalize the spinors, keep in mind the wave portions of free particle wavefunctions are normalized to a delta function. The only constraint placed on this normalization by relativity is that it should be a Lorentz invariant, and so we again normalize to $2E$ particles per unit volume so that the $\gamma$ factors from the energy and the volume element induced under Lorentz transformation cancel one another

$\int \psi^{\dagger}_{\mathbf{p}}\psi_{\mathbf{p}'} \, d^3x=u^{\dagger}u \, \delta^3(\mathbf{p}-\mathbf{p}')=2E \, \delta^3(\mathbf{p}-\mathbf{p}')$

Contract $(u^{(1)})^{\dagger}$ onto $u^{(1)}$ ;

$(u^{(1)})^{\dagger}\cdot u^{(1)}=N^2\Big(1+\frac{p_z^2+p_x^2+p_y^2}{(E+m)^2}\Big)=\frac{2E N^2}{E+m}=2E$

and so we find that

$N=\sqrt{E+m} \quad\mbox{and since}\quad \bar{u}^{(1)}=\sqrt{E+m}\left(\begin{array}{cccc}1&0&\frac{-p_z}{E+m}&\frac{-p_x-ip_y}{E+m}\end{array}\right)$

the contraction of this onto $u^{(1)}$ is

$\bar{u}^{(1)}\cdot u^{(1)}=N^2\Big(1-\frac{p_z^2+p_x^2+p_y^2}{(E+m)^2}\Big)=\frac{2mN^2}{E+m}=2m$

It is easy to show that the contractions below are also true

$(u^{(r)})^{\dagger}u^{(s)}=2E \, \delta^{r,s}=(v^{(r)})^{\dagger}v^{(s)}, \qquad \bar{v}^{(r)}v^{(r)}=-2m$

Home 2.0

In Memoriam: Dirac theory

Related Posts

In Memoriam: Dirac theory

Published by Jeff on April 19, 2022April 19, 2022

Related Posts

Protected: Physics 715: Day-6

Physics 7xx: Cosmic inflation-I

Protected: Virial theorem