Quantum spin chains-II: Reduced density matrices

My go-to programming language for studying tensor states and interacting many-body spin systems used to be octave because of the intuitive way in which it handles tensor products, but I have found that julia is even closer to the way in which physicists work on paper with tensor states.
Tensors and tensor products
We represent spin $1/2$ objects as either kets or with a $2-D$ vector space column
matrix that is a smultaneous eigenstate of $\bm{s}^2$ and $s_z$ : in units with $\hbar=1$

$s_x={1\over 2}\left(\begin{array}{cc} 0 & 1\\ 1 & 0\end{array}\right), \quad s_y={1\over 2}\left(\begin{array}{cc} 0 & -i\\ i & 0\end{array}\right),\quad s_z={1\over 2}\left(\begin{array}{cc} 1 & 0\\ 0 & -1\end{array}\right)$

The basis of the space of spin- $1/2$ wavefunctions is therefore

$|{1\over 2},{1\over 2}\rangle=\left(\begin{array}{c} 1\\ 0 \end{array}\right), \quad |{1\over 2},-{1\over 2}\rangle=\left(\begin{array}{c} 0\\ -1 \end{array}\right)$

since

$s_z\left(\begin{array}{c} 1\\ 0 \end{array}\right)={1\over 2}\left(\begin{array}{c} 1\\ 0 \end{array}\right), \quad s_z\left(\begin{array}{c} 0\\ 1 \end{array}\right)=-{1\over 2}\left(\begin{array}{c} 0\\ 1 \end{array}\right)$

and

$\bm{s}^2=s_x^2+s_y^2+s_z^2={3\over 2}\left(\begin{array}{cc} 1 & 0\\ 0 & 1\end{array}\right)$

$\bm{s}^2\left(\begin{array}{c} 1\\ 0 \end{array}\right)={3\over 4}\left(\begin{array}{c} 1\\ 0 \end{array}\right), \quad \bm{s}^2\left(\begin{array}{c} 0\\ 1 \end{array}\right)={3\over 4}\left(\begin{array}{c} 0\\ 1 \end{array}\right)$

In julia we will represent these as

# "B" is for basis...
B=[[1;0],[0;1]]
# ie B[1]=[1;0]=|1/2,1/2> and B[2]=[0;1]=|1/2,-1/2>

Projection operators in julia. Transpose (hermitian conjugate for real arrays) is denoted with a prime, so we can make a progection operator this way:

$P=|{1\over 2},{1\over 2}\rangle\langle {1\over 2},{1\over 2}|$

# first look at B[1]'
B[1]'
# 1x2 adjoint(::Vector{Int64}) with eltype Int64:
# 1  0

# projector
P=B[1]*B[1]'
P
#2x2 Matrix{Int64}:
# 1  0
# 0  0

psi=[2;3]
P*psi
#2-element Vector{Int64}:
# 2
# 0

What about inner products? 
B[1]'*B[1]
# 1 as expected, the scalar <u(1)|u(1)>

so you can see that the way julia handles kets (vectors) is exactly the way physics do.
Tensors and tensor products are handled using the Kronecker package. In a multi particle system we can use the uncoupled tensor product basis

$|\psi\rangle=|\psi_1\rangle\otimes|\psi_2\rangle\otimes\cdots\otimes|\psi_n\rangle$

and the same for operators

$s_{x,1}=s_x\otimes 1\otimes1\otimes \cdots \otimes 1, \qquad s_{x,2}=1\otimes s_x\otimes 1\otimes \cdots \otimes 1$

and so forth. Basic rules for tensor products: let $|a_i\rangle$ be a basis for the first slot, $|b_j\rangle$ a basis for the second slot
$\bullet$

because $1\otimes v=v$ and scalars can pass through tensor products. This is a vector in the “A” space.
$\bullet$

This is a vector in the “B” space.
$\bullet$

which is a scalar.
How are these done in julia? After defining vectors $A,B$ and a unit matrix

# make a vector in each space
A=[1;2]
B=[1;-1]
# create basis "a" for the first slot and "b" for the second
a=[[1;0],[0;1]]
b=[[1/sqrt(2);1/sqrt(2)],[-1/sqrt(2);1/sqrt(2)]]
One=[1 0; 0 1]
# project the second slot 
(One⊗b[1]')*(A⊗B)
# 0.0
# 0.0
# since you can see that B is in the b[2] state
(a[1]'⊗ One)*(A⊗ B)

Density matrices
Let’s construct the Hamiltonian

$H=s_x\otimes s_x+s_y\otimes s_y+s_z\otimes s_z=\mathbf{s}_1\cdot\mathbf{s}_2$


H=real.(sx⊗sx+sy⊗sy+sz⊗sz)
eigvals(H)
#4-element Vector{Float64}:
# -0.75
#  0.25
#  0.25
#  0.25

# and get the ground state wavefunction
psi0=eigvecs(H)[:,1]
# it's energy expectation value
psi0'*H*psi0
# -0.75

Remember this is $|\psi_0\rangle$ . Create its density matrix $\rho=|\psi_0\rangle\langle \psi_0|$


rho=psi0⊗psi0';
# and finally construct the reduced density matrix for spin one, by 
# tracing out all of the states of spin number 2 
rho01=sum( ((One⊗ b[j]')*psi0)⊗ ((One⊗ b[j]')*psi0)' for j in 1:2)
# What is the expectation value of s_z for the first spin when 
# the two spin system is in the ground state?
prob=tr(rho01*sz)
# 0 of course
# What is the probability that spin one will be found in the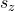  
# "up" eigenstate when the two spin system is in the ground state?
#  I will use my "a" basis above... to creat a projection operator
prob=tr(rho01*(a[1]⊗a[1]'))
# 0.5, of course

This is because

$|\psi_0\rangle={1\over \sqrt{2}}\Big(\left(\begin{array}{c}0\\ 1\end{array}\right)\otimes \left(\begin{array}{c}1\\ 0\end{array}\right)+\left(\begin{array}{c}1\\ 0\end{array}\right)\otimes \left(\begin{array}{c}0\\ 1\end{array}\right)\Big)$

(a maximally entangled Bell state)

As another example let’s study a $4$ -spin chain with

$H=\mathbf{s}_1\cdot\mathbf{s}_2+\mathbf{s}_2\cdot\mathbf{s}_3+\mathbf{s}_3\cdot\mathbf{s}_4$

and regard the leftmost two spins ( $\#1,2$ ) as the “system” $S$ and the third and forth spin as an “environment” $E$ . The second term in the Hamiltonian couples $S$ to $E$ . We will find the ground state (again the largest magnitude energy eigenvalue), and compute the reduced density matrix for $S$ by “integrating out” the environment states.

Hamiltonian=function(N::Int64)
sx=[0 1;1 0]
sy=[0 -im; im 0]
sz=[1 0; 0 -1]
u=[1 0; 0 1]
P=real.(sx⊗sx +sy⊗sy+sz⊗sz);
H=P;
Lend=P
for k=1:(N-2)
H=H⊗u+u⊗Lend;
Lend=u⊗Lend;
end
H/4.0
end

h=Heisenberg(4)
eigvals(h)
#16-element Vector{Float64}:
# -1.6160254037844382
# -0.9571067811865477
# -0.9571067811865477
# -0.9571067811865475
#-0.2500000000000001
# ... and so forth. It is the largest mag. one we want

psi0=eigvecs(h)[:,1];
psi0'*h*psi0
# -1.6160254037844384 expectation of the energy for the gs,
# Make a basis for E
U=[[1;0]⊗[1;0],[1;0]⊗[0;1],[0;1]⊗[1;0],[0;1]⊗[0;1]]
# make a unit matrix for  S
u4=One⊗One
# make the reduced density matrix
rho_S=round.(sum(((u4⊗U[j]')*psi0)⊗((u4⊗U[j]')*psi0)' for j in 1:4),digits=8)
#4×4 Matrix{Float64}:
#  0.0223291  -0.0        0.0        0.0
# -0.0         0.477671  -0.455342   0.0
#  0.0        -0.455342   0.477671  -0.0
#  0.0         0.0       -0.0        0.0223291

# note that its trace is one.

Suppose that there exists a new set of basis states for the system $S$ such that in this new basis the matrix of $\rho_S$ is diagonal, then

$\rho_S=\sum_i w_i |i\rangle\langle i|$

in this new basis $\{|i\rangle\}$ of $S$ and then

$Tr\rho_S=\sum_j\langle j|\hat{\rho}|j\rangle=\sum_{ij}|\langle i|j\rangle|^2 w_i=\sum_{ij}\delta_{ij}w_i=\sum_j w_j$

What are the properties of $\rho_S$ ?
$\bullet$ Let $A=1$ (the unit operator on $S$ ) then

$\langle A\rangle=1=Tr(\rho_S \, A)=Tr \, \rho_S=\sum_i w_i$

(we used this previously to compute $s_z$ probabilities).
$\bullet$ Let $A=|j\rangle\langle j|$ a projection operator for $S$ . Extend it to act on the universe $S\bigcup E$ , $A\rightarrow A\otimes 1$ and call $e_j$ a basis for $E$

since the right side is a sum of squares. Note that I wrote our ground state $|\psi_0\rangle$ as an entangled tensor of $S$ and $E$ states.
$\bullet$ Let $|j\rangle$ be an eigenvector of $\rho_S$ ;

$\langle A\rangle=\sum_i\langle i|\rho_S A|i\rangle$

insert unity $1=\sum_j|j\rangle\langle j|$ (sum over the entire complete set);

$\langle A\rangle=\sum_{ij}\langle i|\rho_S|j\rangle\langle j|A|i\rangle=\sum_{ij}w_j \, \langle i|j\rangle\langle j|A |i\rangle=\sum_j w_j \, \langle j|A|j\rangle$

According to the postulates of quantum mechanics we interpret $w_j$ as the probability that the system is in state $|j\rangle$ .

Home 2.0

Quantum spin chains-II: Reduced density matrices

Related Posts

Quantum spin chains-II: Reduced density matrices

Published by Jeff on October 2, 2021October 2, 2021

Related Posts

Genetic algorithms

Linear equation solvers by LU decomposition

Parallel programming: Heat equation with pthreads