Proofs of the PEP are presented using Lorentz transformation properties of two-point or Wightman functions in courses like 732 and 831. That is the current fashion. In the 732 and 831 courses taught by my thesis advisor, Adam Bincer, a more intuitive and enlightening proof was given. This “old school” proof was deeply tied into the Dirac sea vacuum concept, and it worked like this…
We need to go to the “second quantization” or QFT formalism, because the Dirac equation and Dirac sea vacuum describe a system with variable numbers of quanta.
First a suitable Lagrangian density must be found, such that
![\[\partial_{\mu}\Big(\frac{\partial \mathcal{L}}{\partial(\partial_{\mu}\psi)}\Big)=\frac{\partial \mathcal{L}}{\partial \psi}, \qquad \partial_\mu={\partial\over \partial x_\mu} \]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-a5bcf5167fef469a70ec9a6d90c9a17e_l3.png "Rendered by QuickLaTeX.com")
is the Dirac equation. A suitable choice is
![\[\mathcal{L}=-\bar{\psi}(i\gamma\cdot \nabla+m)\psi \]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-f8a4cdbdb6fa0b92f5c01c36eeb8bed1_l3.png "Rendered by QuickLaTeX.com")
from which we compute the conjugate momentum
![\[\pi=\frac{\partial \mathcal{L}}{\partial\dot{\psi}}=i\psi^{\dagger}=i\bar{\psi}\gamma^0 \]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-dad4fa44c477d51bdbad5b364ffa492b_l3.png "Rendered by QuickLaTeX.com")
and the object that we need most, the Hamiltonian density
![\[\mathcal{H}=\pi\dot{\psi}-\mathcal{L}=-i\pi\gamma^0(\mathbf{\gamma}\cdot\bm{\nabla}+m)\psi=\psi^{\dagger}(-i\mathbf{\alpha}\cdot\bm{\nabla}+\beta m)\psi =\psi^{\dagger} \, i\frac{\partial}{\partial t} \psi \]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-f91f5f2f5458d5a91e96ef541867eb7e_l3.png "Rendered by QuickLaTeX.com")
Quantize the field by replacing fundamental Poisson brackets with commutators and expanding the field in terms of the solutions to the Dirac wave equation, but we normalize the field a bit differently
![\[f^s_k=\sqrt{\frac{m}{E_k}}u^s_k \, e^{ikx}, \qquad g^s_k=\sqrt{\frac{m}{E_k}}v^s_k \, e^{-ikx}, \quad kx=\mathbf{k}\cdot\mathbf{x}-E_k t\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-1fdad14eee127a1d4cab6c5adeb00e8b_l3.png "Rendered by QuickLaTeX.com")
Fourier expand the fields (call the quantized 
appearing in our Lagragian density 
) in annihilation/creation operators for particle states 
and hole states 
![\[\hat{\Psi}=\sum_k\sum_{s=1,2}\Big(\hat{c}^s_k \, f^s_k+(\hat{d}^s_k)^{\dagger} \, g^s_k\Big) \]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-6f4759958cc19bcd1bd2ca640659b276_l3.png "Rendered by QuickLaTeX.com")
The orthogonality of the spinors 
and 
allows us to obtain
![\[\hat{c}^s_k=\int d^3x \, \bar{f^s_k}\gamma^0 \, \hat{\Psi}, \quad (\hat{c}^s_k)^{\dagger}=\int d^3x \, \hat{\bar{\Psi}}\gamma^0 f^s_k=\int d^3x \, \hat{\pi} \, f^s_k \]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-14193236d6cf28b020213adc371fa3d9_l3.png "Rendered by QuickLaTeX.com")
![\[\hat{d}^s_k=\int d^3x \, \hat{\Psi} \gamma^0 g^s_k, \qquad (\hat{d}^s_k)^{\dagger}=\int d^3x \, \bar{g^s_k}\gamma^0 \Psi \]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-6ce7028d86c0c0de631eb6f28383d3cd_l3.png "Rendered by QuickLaTeX.com")
We now compute the Hamiltonian from its density
![\[\hat{H}=\int d^3x \, {\mathcal{H}}\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-0e17195e1b055eaf54f135f814fd8190_l3.png "Rendered by QuickLaTeX.com")
![\[=\int d^3x \, \sum_{k,k'}\sum_{r,s}\sqrt{\frac{m^2}{E_k E_{k'}}} \Big( (\hat{c}^s_k)^{\dagger} \, (f^s_k)^{\dagger}+\hat{d}^s_k \, (g^s_k)^{\dagger}\Big) \, i\frac{\partial}{\partial t} \Big(\hat{c}^r_{k'} \, f^r_{k'}+(\hat{d}^r_{k'})^{\dagger} \, g^r_{k'}\Big) \]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-dfad572a4e971d8a33d7450be131df07_l3.png "Rendered by QuickLaTeX.com")
Use the orthogonality relations for the Dirac spinors
![\[\int d^3x \frac{1}{\sqrt{E_k E_{k'}}} \, \bar{u^s_k} \, u^r_{k'} \, e^{i(kx-k'x)}=\delta^{r,s}\delta_{k,k'} \]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-9fa81a1d29fa56bdaa67a478f712dd00_l3.png "Rendered by QuickLaTeX.com")
then
![\[\hat{H}= \sum_{k}\sum_{s} \, E_{k} \, \Big((\hat{c}^s_k)^{\dagger}\hat{c}^s_{k}-\hat{d}^s_k(\hat{d}^s_k)^{\dagger}\Big) \]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-aa85f204f1e7b7f86faccd45282652a6_l3.png "Rendered by QuickLaTeX.com")
This has a nasty negative sign, we certainly want a spectrum that is bounded below in energy. Without that, no system of Dirac particles could ever be stable against decay into a lower energy state by perpetual emission of radiation!
The first term in the Hamiltonian, if the 
-operators can be interpreted as creation/annihilation operators, will count the number of excitations of electron states and add up their energies since 
is the usual oscillator number operator. This will give a positive number. The second term can be manipulated into a similar form, but if
![\[[\hat{c}^s_k,(\hat{c}^r_{k'})^{\dagger}]=\delta^{rs}\delta_{kk'}, \qquad [\hat{d}^s_k,(\hat{d}^r_{k'})^{\dagger}]=\delta^{rs}\delta_{kk'} \]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-0d142984568cd8fb4bc82b16636d032c_l3.png "Rendered by QuickLaTeX.com")
we are in trouble, since we obtain
![\[\hat{H}=\sum_{k,s} E_k \Big((\hat{c}_k^s)^{\dagger} \hat{c}_k^s-(\hat{d}_k^s)^{\dagger} \hat{d}_k^s-1\Big) \]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-1464269b3de4b03ee884df6ead098af5_l3.png "Rendered by QuickLaTeX.com")
We certainly understand the last term, it is the infinite negative energy of the vacuum, which we set to be our zero point of energy. Unfortunately the energy of a hole created and counted by the hole-number operator 
is positive and their number operator has a sign that causes their creation to lower the energy.
There is an alternative, quantize the annihilation and creation operators with a different algebraic relation, anticommutators. If we instead use
![\[\{\hat{c}^s_k,(\hat{c}^r_{k'})^{\dagger}\}=\delta^{rs}\delta_{kk'}, \qquad\{\hat{d}^s_k,(\hat{d}^r_{k'})^{\dagger}\}=\delta^{rs}\delta_{kk'}, \qquad \{\hat{d}^s_k,(\hat{c}^r_{k'})^{\dagger}\}=0 \]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-b67c89de1f0a93e672328caaf73588c6_l3.png "Rendered by QuickLaTeX.com")
then the Hamiltonian becomes
![\[\hat{H}=\sum_{k,s} E_k \Big((\hat{c}_k^s)^{\dagger} \hat{c}_k^s+(\hat{d}_k^s)^{\dagger} \hat{d}_k^s-1\Big) \]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-3a88fe58e20f9ee6dbc68d0f23b7be51_l3.png "Rendered by QuickLaTeX.com")
and all of our physical states, states with arbitrary numbers of particles, have positive energy relative to the vacuum. We can summarize the correspondence principle thusly:
To quantize scalar fields, the Hamiltonian is positive for all excitations of the vacuum if
![\[[\hat{\Phi}(x,t),\hat{\Pi}(x',t)]= \delta(x-x') \]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-903a1ac88f60671d0b8d4689f94b7799_l3.png "Rendered by QuickLaTeX.com")
such fields are called Bose-Einstein fields.
To quantize Dirac particle fields replace all fundamental Poisson brackets with
![\[\{\hat{\Psi}(x,t),\hat{\bar{\Psi}}(x',t)\}\sim\delta(x-x') \]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-d8177a9135826fd6a6579e35e6e519a6_l3.png "Rendered by QuickLaTeX.com")
in order to make the Hamiltonian positive relative to the vacuum for all excitations of the vacuum. Such fields are called Fermi-Dirac.
To quantize the Fermi-Dirac excitations we enforce the algebra on the annihilation-creation operators that generate the spectrum
(1) 
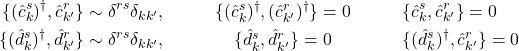
In the second equation set 
and 
![\[2(\hat{c}^s_k)^{\dagger}(\hat{c}^s_k)^{\dagger}=0, \qquad \Big((\hat{c}^s_k)^{\dagger}\Big)^2=0, \qquad \Big((\hat{d}^s_k)^{\dagger}\Big)^2=0\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-d315a837c3f27a4f4a5bde07241026f5_l3.png "Rendered by QuickLaTeX.com")
application of this to the vacuum shows that you cannot have two excitations of the same momentum and spin in the quantization volume at the same time. This is the Pauli Exclusion Principle.
Adam’s (1930-Nov. 8, 2016) QFT lectures were remarkable for their elegance, economy, and clarity. Perhaps he learned these qualities as a survivor of the German invasion of the Ukraine in Sept. 1941, and years as an internal refugee in the Soviet Union. Perhaps they were innate.