Many modern lattice problems (six-vertex, eight-vertex, Ising, Heisenberg-XYZ) can be solved by obtaining eigenvalues of the transfer matrix or Hamiltonian by the Bethe ansatz. This is a very general method for solving certain classes of very large eigenvalue problems.
We use as an example the quantum -XX model: a spin chain with nearest neighbor dipole-dipole interactions
![Rendered by QuickLaTeX.com \[H=-J\Big({\hbar\over 2}\Big)^2\sum_{i=1}^{N, \, PBC} \Big(\sigma_i^- \sigma_{i+1}^+ + \sigma_i^+ \sigma_{i+1}^-\Big), \qquad \{\sigma_i^+, \sigma_i^-\}=1\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-623534d3faa339ace705348995091889_l3.png)
![]()
and ![]() if
if ![]() . Bethe developed the technique to solve the
. Bethe developed the technique to solve the ![]() model, add a term
model, add a term ![]() onto the Hamiltonian above. His method has become a mainstay of many-body and statistical physics.
onto the Hamiltonian above. His method has become a mainstay of many-body and statistical physics.
Let me remind you that what we mean by ![]() is
is
![]()
with the Pauli spin matrix in the ![]() slot. Denote eigenstates of
slot. Denote eigenstates of ![]() by
by
![]()
![]()
![]()
First we work out a few useful identities. Acting on two-particle spin tensors
(1) 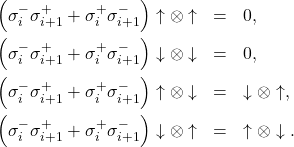
The ansatz (the goal of which is to produce all eigenvectors and eigenvalues of ![]() ) has several stages.
) has several stages.
![]() 1. Establish a “vacuum” and “first excited” state spectrum.
1. Establish a “vacuum” and “first excited” state spectrum.
Beginning with a lowest ![]() eigenvalue state (we refer to this as our Bethe vacuum)
eigenvalue state (we refer to this as our Bethe vacuum) ![]() , create a “singly excited state” by flipping one spin, for example the
, create a “singly excited state” by flipping one spin, for example the ![]()
![]()
and prove that
![]()
Let’s call ![]() and rewrite in terms of actual spin operators. Every term in
and rewrite in terms of actual spin operators. Every term in ![]() kills
kills ![]() so
so ![]() , but
, but
![]()
![]()
![]()
Apply ![]() to
to
![]()
take inner products ![]() with both sides
with both sides
![]()
![]()
We have seen this recursion relation in 711 in our studies of normal modes: the ansatz ![]() gives
gives ![]()
for which periodic boundary conditions ![]() forces
forces ![]() , so
, so ![]() with wavenumbers labeled by
with wavenumbers labeled by ![]() . This is why I present the periodic simple atomic chain in 711, to prepare you for learning the Bethe ansatz first step.
. This is why I present the periodic simple atomic chain in 711, to prepare you for learning the Bethe ansatz first step.
Our first excited state spectrum is ![]() , an “optical branch” dispersion relation.
, an “optical branch” dispersion relation.
![]() 2. Progress to the doubly excited states. This is a critical step in which the “ansatz equation” is obtained. Formulate doubly excited states (two flipped spins)
2. Progress to the doubly excited states. This is a critical step in which the “ansatz equation” is obtained. Formulate doubly excited states (two flipped spins)
![]()
and propose Hamiltonian eigenfunctions
![]()
and prove that the secular equations are
(2) 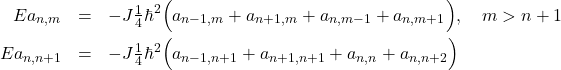
in which the coefficients ![]() are for absurd/forbidden terms
are for absurd/forbidden terms ![]() which we retain since they are a critical part of the ansatz. These are called “unwanted” terms. The condition that eliminates the unwanted terms is where the magic lies.
which we retain since they are a critical part of the ansatz. These are called “unwanted” terms. The condition that eliminates the unwanted terms is where the magic lies.
Here it goes:
![]()
first let ![]() so the two flipped spins are not nearest neighbors, there will be four terms in
so the two flipped spins are not nearest neighbors, there will be four terms in ![]() that do not annihilate
that do not annihilate ![]() ;
; ![]() ,
, ![]() ,
,![]() ,
, ![]() , so application oh
, so application oh ![]() to
to ![]() followed by inner products
followed by inner products ![]() gives the first of
gives the first of
(3) 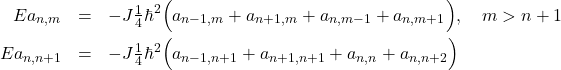
We can simply set ![]() in the first equation to get the second, but the second is not the correct Hamiltonian action on
in the first equation to get the second, but the second is not the correct Hamiltonian action on ![]() , that would be
, that would be ![]() since only
since only ![]() and
and ![]() do not annihilate
do not annihilate ![]() .
.
The secret of the Bethe ansatz is to apply ![]() operators to every
operators to every ![]() abstractly, without regard to physical meaning of
abstractly, without regard to physical meaning of ![]() . Think of
. Think of ![]() as an abstract tensor and
as an abstract tensor and ![]() as a label permutation and nothing more.
as a label permutation and nothing more.
Then we demand that the true ![]() equation agree with the naive version gotten from the general
equation agree with the naive version gotten from the general ![]()
![]() which results in an identity (our ansatz equation)
which results in an identity (our ansatz equation)
![]()
(this identity is usually much more complex than in this example, which is probably the simplest in its category).
![]() 3. Don’t just take
3. Don’t just take ![]() . Instead propose a form
. Instead propose a form
![]()
( ie a sum over permutations of the products of the wavenumbers). Take
![]()
![]()
where ![]() is the identity permutation and here
is the identity permutation and here ![]() the transposition. This leads to
the transposition. This leads to
![]()
![]()
the latter two are incompatible, forcing ![]() to be the solution to the first equation (again, this is usually quite complex), and the solutions to the second must be (
to be the solution to the first equation (again, this is usually quite complex), and the solutions to the second must be (![]() and
and ![]() are independent exponentials)
are independent exponentials)
![]()
![]()
independent of one another. Usually there is a complicated relation between the wavenumbers ![]() . Note that this tells us that coefficients of terms in the proposed wavefunction have opposite signs if the particle labels in the two terms are switched (a wavefunction antisymmetric under particle label transpositions).
. Note that this tells us that coefficients of terms in the proposed wavefunction have opposite signs if the particle labels in the two terms are switched (a wavefunction antisymmetric under particle label transpositions).
![]() 4. The final stage of the Bethe ansatz is to assume that higher-order excitations Bethe ansatz wave-functions are
4. The final stage of the Bethe ansatz is to assume that higher-order excitations Bethe ansatz wave-functions are
![]()
![]()
and the ansatz conditions lead to
![]()
in which ![]() is a permutation of the
is a permutation of the ![]() labels, and
labels, and ![]() is the permutation gotten by switching labels
is the permutation gotten by switching labels ![]() and
and ![]() after permuting by
after permuting by ![]() . Can you see where this comes from? This is the crux of the technique, and you might see it more readily if you explicitly write out the details for a triple excitation, but this is rarely done.
. Can you see where this comes from? This is the crux of the technique, and you might see it more readily if you explicitly write out the details for a triple excitation, but this is rarely done.
This wavefunction describes a system of free fermions ( because the wave-function is antisymmetric under the interchange of any pair of up-spin location labels). If ![]() decomposes into
decomposes into ![]() successive relative transpositions,
successive relative transpositions, ![]()
and the Bethe wave-function is the Slater determinant ![]() ,
, ![]()
![]()
In the spirit of the ansatz we would show that for ![]() -fold excitations
-fold excitations
![Rendered by QuickLaTeX.com \[E=-J\tfrac{1}{4} \hbar^2\sum_{k=1}^2 \Big(\xi_{k}+\xi_{k}^{-1}\Big)\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-ef34240ed94cbb5886edb827f2b5f132_l3.png)
and assume that the result carries over to ![]() -fold excitations. Note that
-fold excitations. Note that
(4) 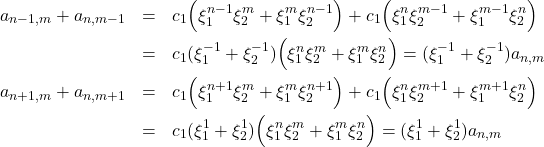
Adding these and substituting into the secular equation for ![]() lets you cancel
lets you cancel ![]() to get
to get
![]()
which is a sum of two single excitations but with different wavenumbers. We suspect then that
![Rendered by QuickLaTeX.com \[E=-J\tfrac{1}{4} \hbar^2\sum_{k=1}^r \Big(\xi_{k}+\xi_{k}^{-1}\Big)\]](http://abadonna.physics.wisc.edu/wp-content/ql-cache/quicklatex.com-d27ed24d918dc3552d59de74e6d154a0_l3.png)
An English translation of Bethe’s original Zeits f. Physik 71, 205 (1931) paper appears in Daniel C. Mattis {\it The Many-Body Problem}, World Scientific, (1993), p. 689.